Machineboy空
게임 콘텐츠의 제작 원리 2-3. 선 본문
1. 아핀 공간에서의 점의 조합
앞서서 아핀 공간에서의 점 + 점의 연산은 불가능하였다. * 시각 + 시각의 연산과 같은 것
그런데 스칼라를 보조로 사용해 다음과 같은 조합식을 만들어 보자.
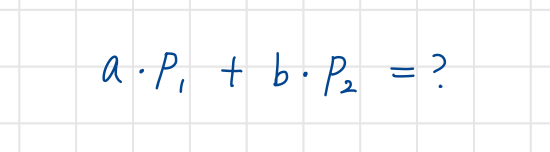
2차원의 점이라고 가정할 경우 위 조합식은 다음과 같이 전개된다.
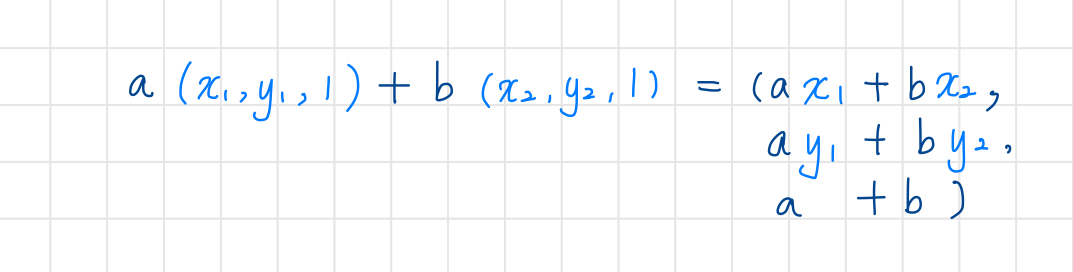
이 때 위 결과가 점이 되기 위해서는 마지막 차원 값이 반드시 1이 되어야 한다.
따라서 다음의 수식이 성립한다.
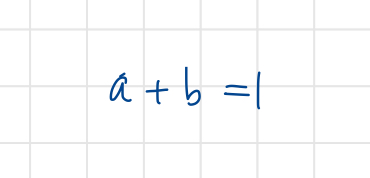
이를 원 식에 대입하면 다음의 식이 만들어지며 이는 점을 보장해주며,
a값에 따라 무수히 많은 점을 만들어낼 수 있다.

점과 점의 연산은 불가능하지만, 스칼라를 이용해서 새로운 점을 만들어내는 식을 아핀 조합이라고 한다
아핀 조합의 수식
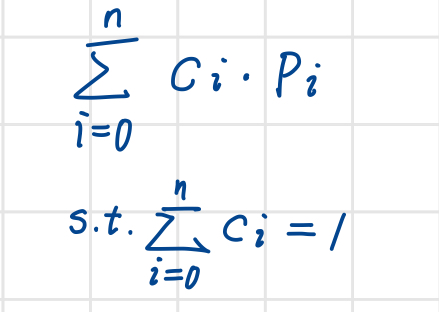
아핀 조합에 따른 점의 생성
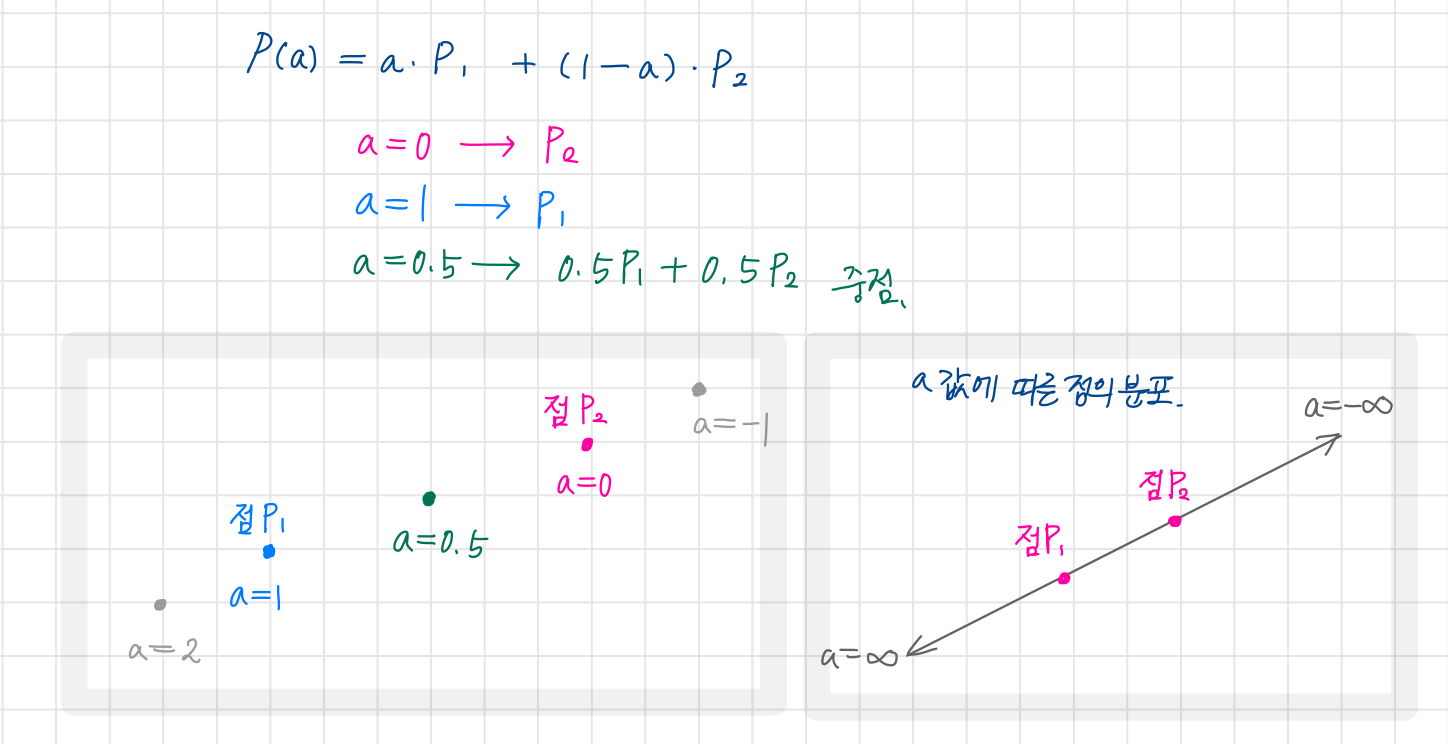
a값에 따라 생성된 점들이 위 그림과 같은 선상에 있음을 어떻게 증명할 수 있을 것인가?

벡터와 스칼라의 곱셈은 같은 기울기를 가진 직선 위에 만들어진다.
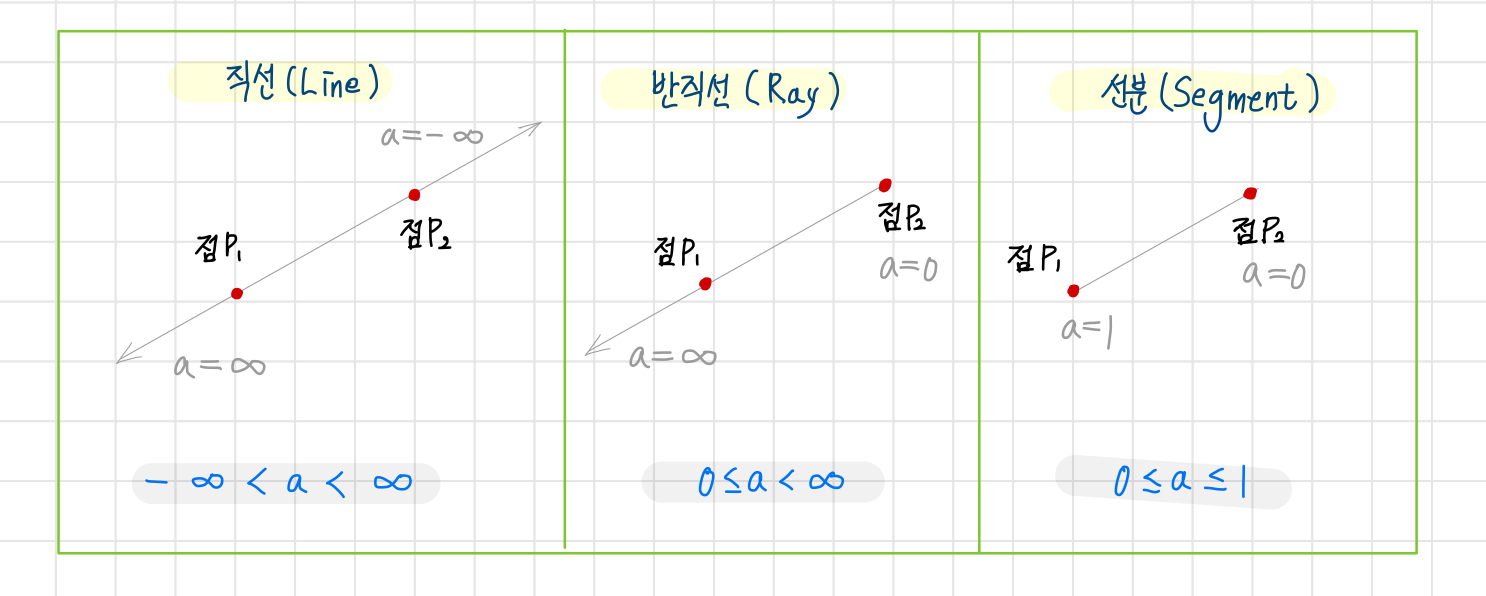
선의 종류
- 직선: 하나의 기울기를 가지고 무한대에서 무한대로 뻗어나가는 것
- 반직선: 하나의 점을 고정하고 한쪽만 무한대로 뻗어나간다.
- 선을 발사, 무언가 탐지할 때 많이 쓰임
- ex. Raycasting, RayTracing
- 선분: 끝과 시작이 명확하다.
- 반직선과 직선 모두 무한대로 뻗어가기 때문에, 그리기엔 적절하지 않지만 선분은 적절
2. 점의 표현
스크린 좌표계
화면은 픽셀들로 구성되어 있으며 다음과 같은 좌표계를 사용하여 픽셀의 위치를 관리한다.
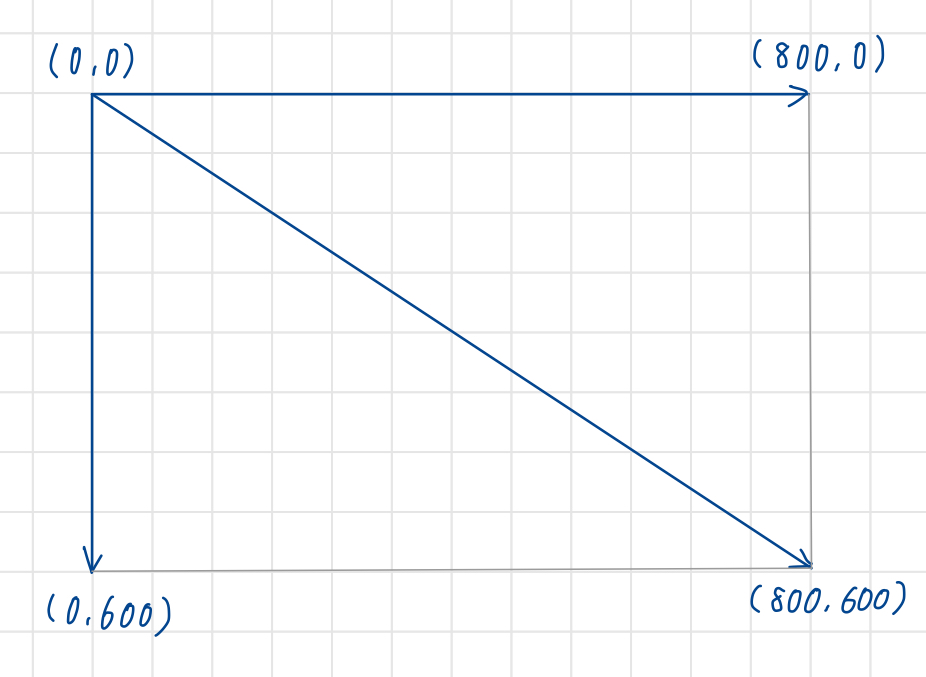
수학에서 사용하는 데카르트 좌표계와 스크린 좌표계의 차이를 정리하면 다음과 같다.
| 데카르트 좌표계 | 스크린 좌표계 |
| 실수 R | 양의 정수 H |
| 오른손 좌표계 (우상방향 증가) | 왼손 좌표계(우하방향 증가) |
| 연속성 | 이산성 |
픽셀화(Rasterization)
물체의 형상을 픽셀로 변환해 표현하는 작업
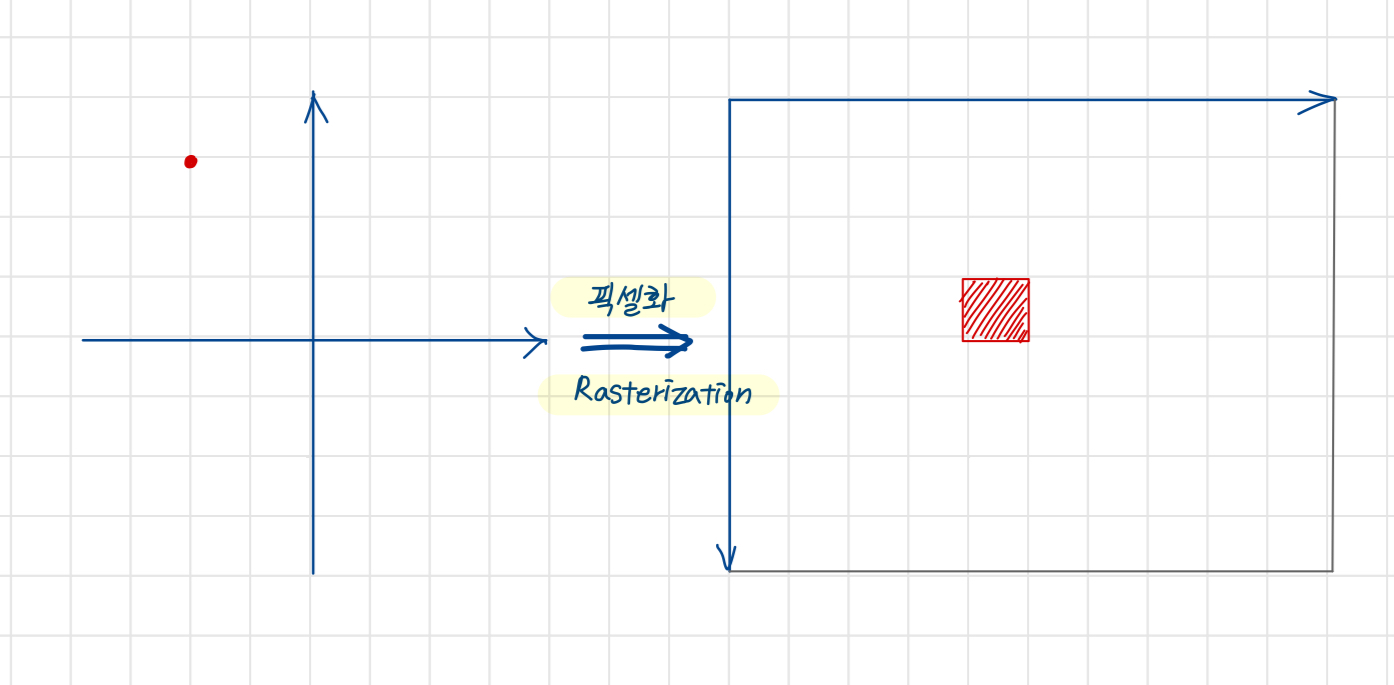
화면의 해상도가 짝수인 경우(0,0)을 표현하는데 한계가 발생한다.
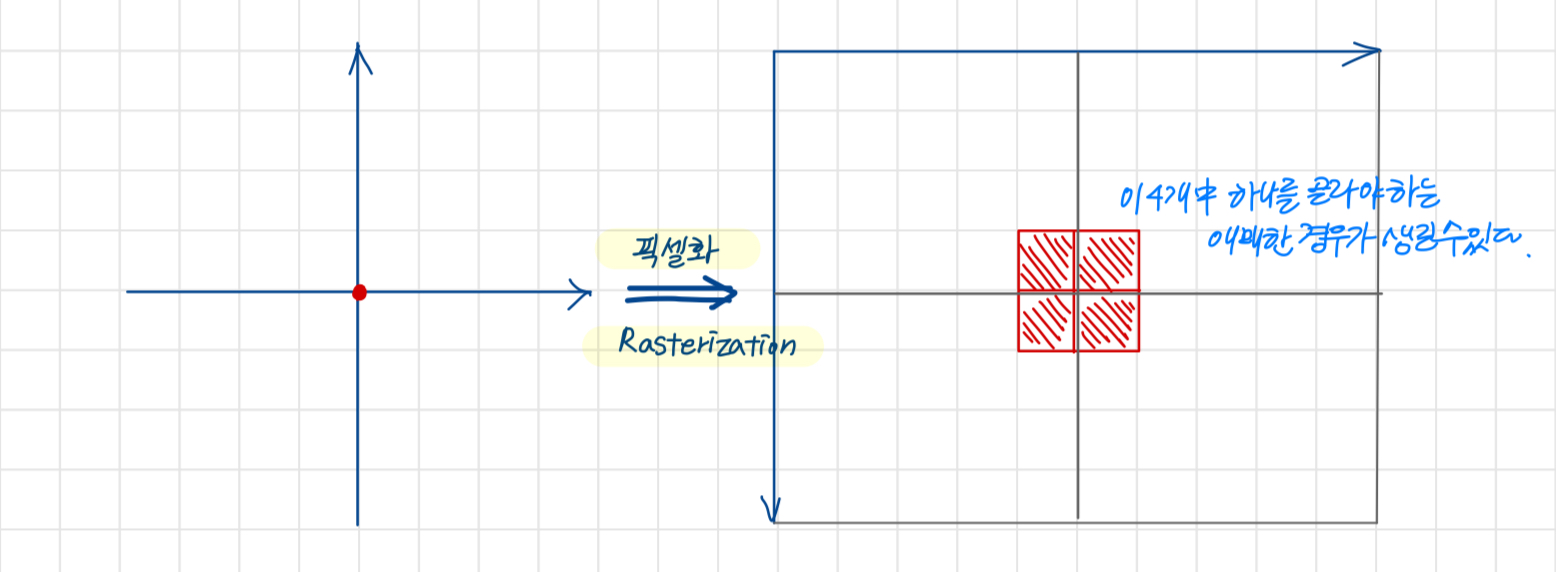
이 경우에는 지정된 규칙에 따라 네 개 중 하나의 픽셀을 선택할 수 밖에 없음.
4개 중 하나를 선택하는 수식을 만들어야 함. → Rasterization Rule
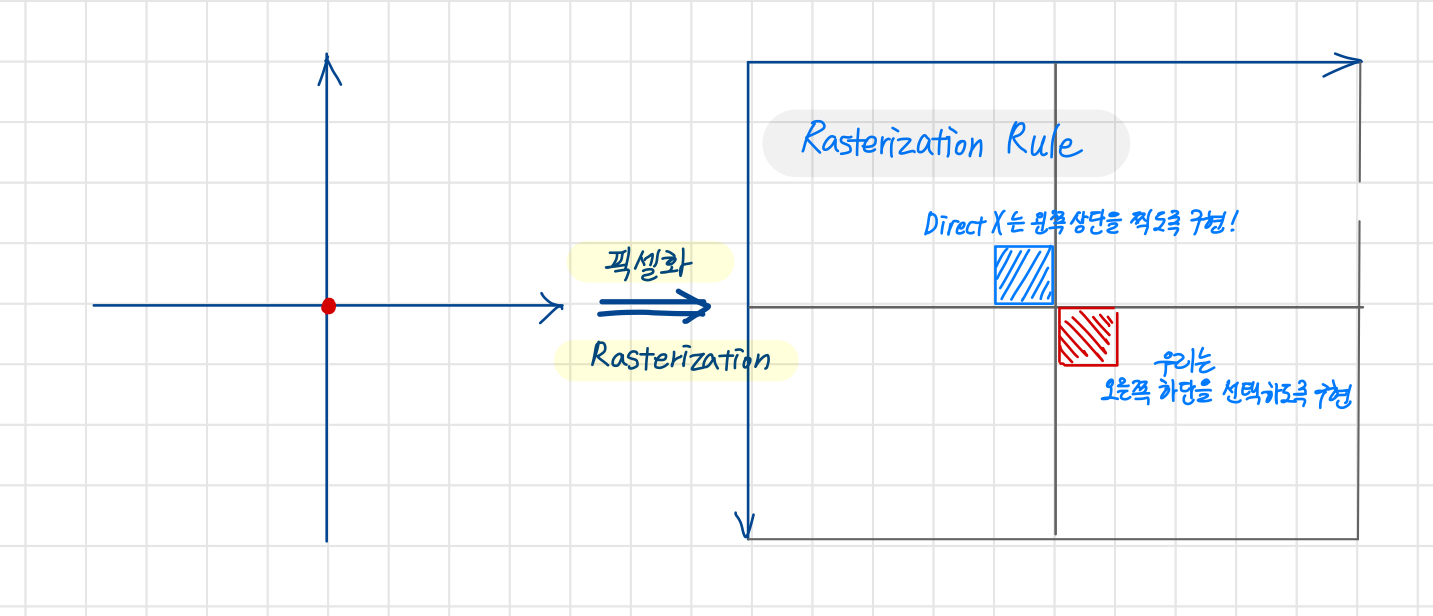
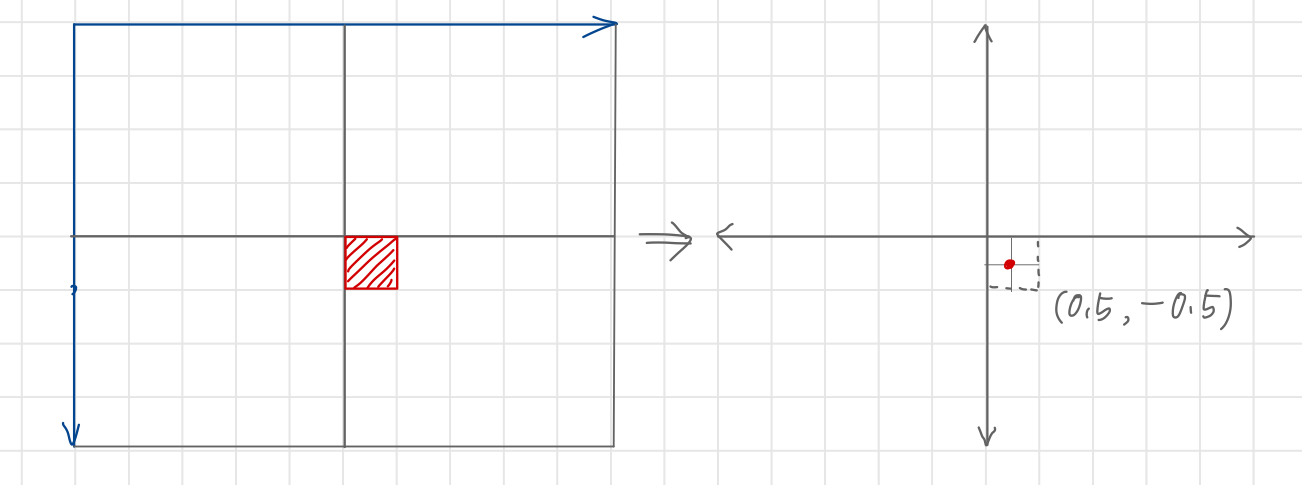
픽셀을 벡터로 변환할 때에는 (픽셀을 데카르트 좌표계로 변환할 때는)
픽셀 영역 내 하나의 대표값을 지정해야 한다.
3. 선 그리기 알고리즘(브레젠험 알고리즘)
직선의 방정식으로 그리기
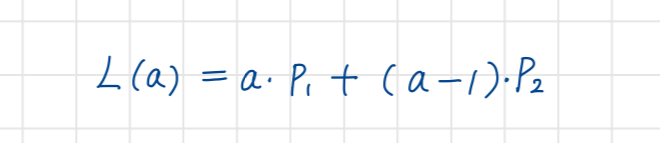
이론적으로는 다음과 같이 그릴 수 있으나 실용적인 방법은 아니다. 컴퓨터 과부하일어날 것
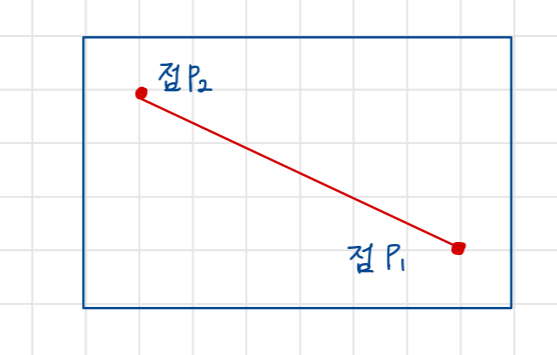
브레젠험 알고리즘
1962년도에 고안된(컴퓨터가 실수 연산도 버거워하던 시절)
정수 연산만을 사용해 빠르게 선을 그리는 알고리즘이다.
중점(Mid-point)알고리즘이라고도 한다.
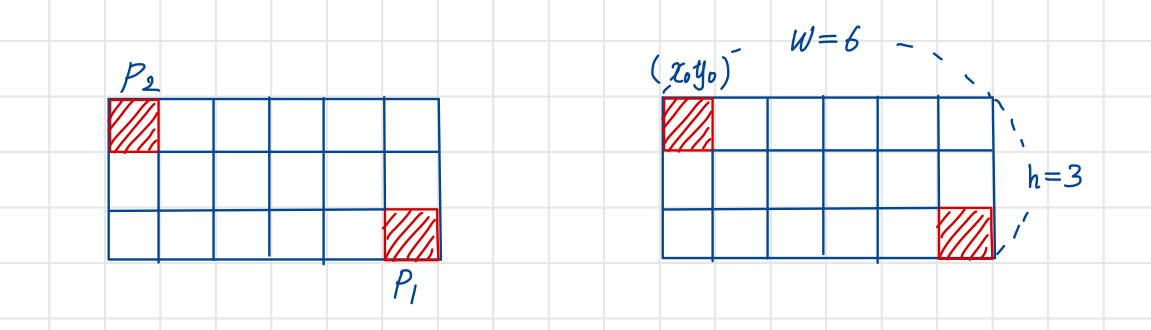
브레젠험 알고리즘의 구현 방법
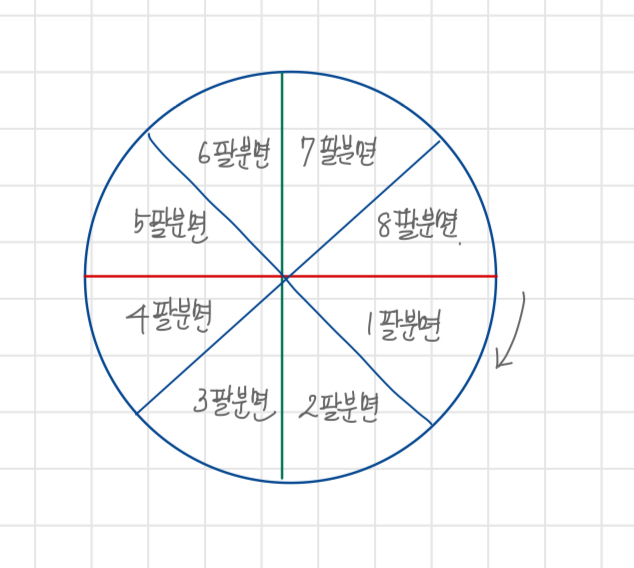
화면 공간을 8등분하고 1~8분면(Octant)으로 나눈다.
직선의 방정식은 다음과 같다.
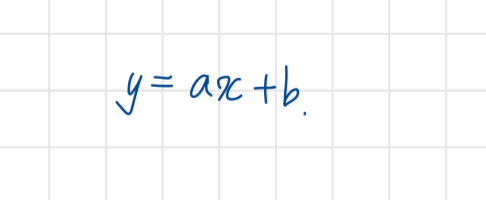
정수로 된 스크린 좌표계의 두 점의 좌표가 주어졌을 때 다음의 정보가 주어진다.
- Width(너비): x1 - x0
- Height(높이): y1 - y0
- x0,y0(시작 점의 좌표)
이를 바탕으로 위의 방정식을 변형해보자.
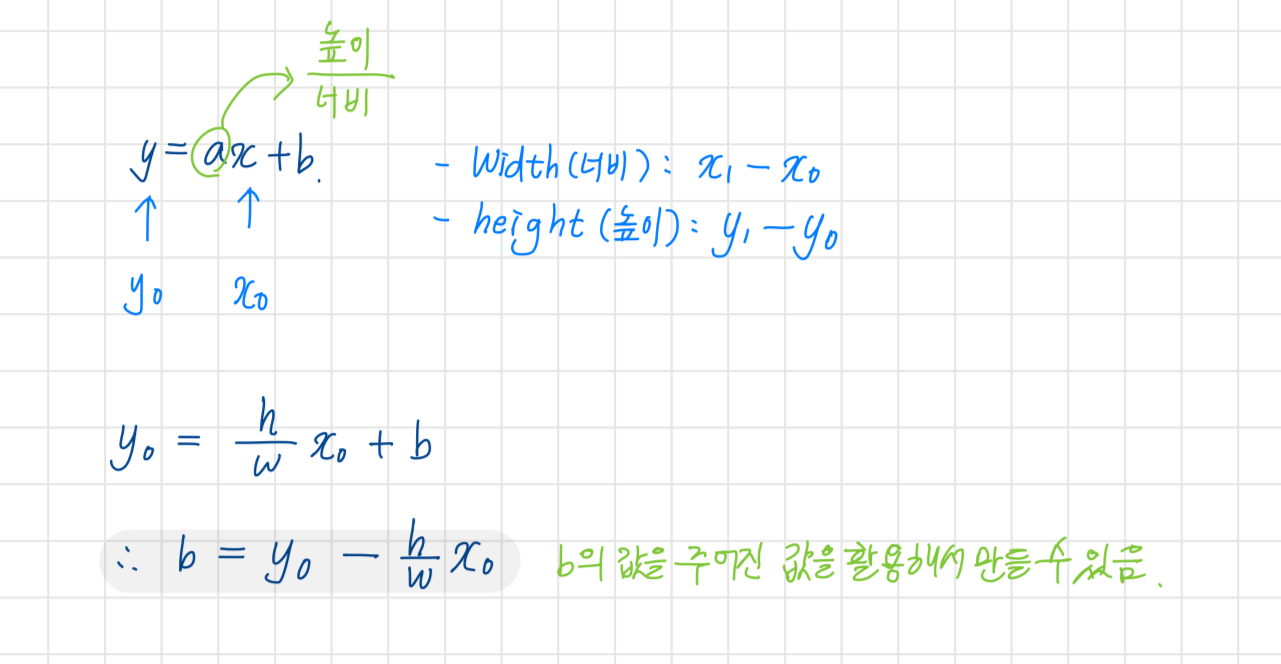
제 1팔분면
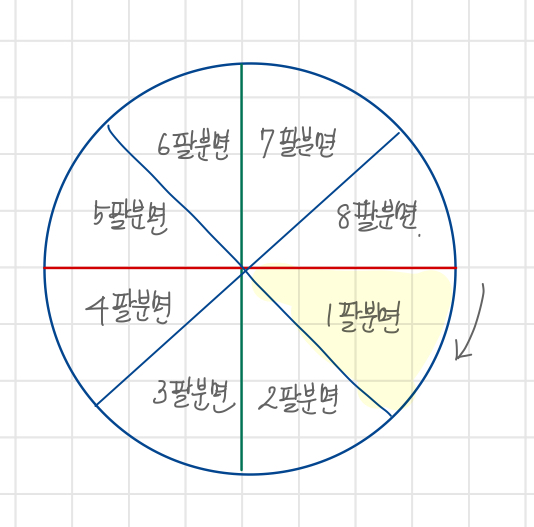
해당 영역에서는 기울기가 1을 넘어설 수 없는 특징을 가진다.
그렇기 때문에 평행이동하거나 1칸 아래로 이동하는 동작만 발생된다.
시작점을 찍은 후 다음 점이 평행 이동하는지 한칸 아래로 내려가는지는 중점값을 보고 판단한다.
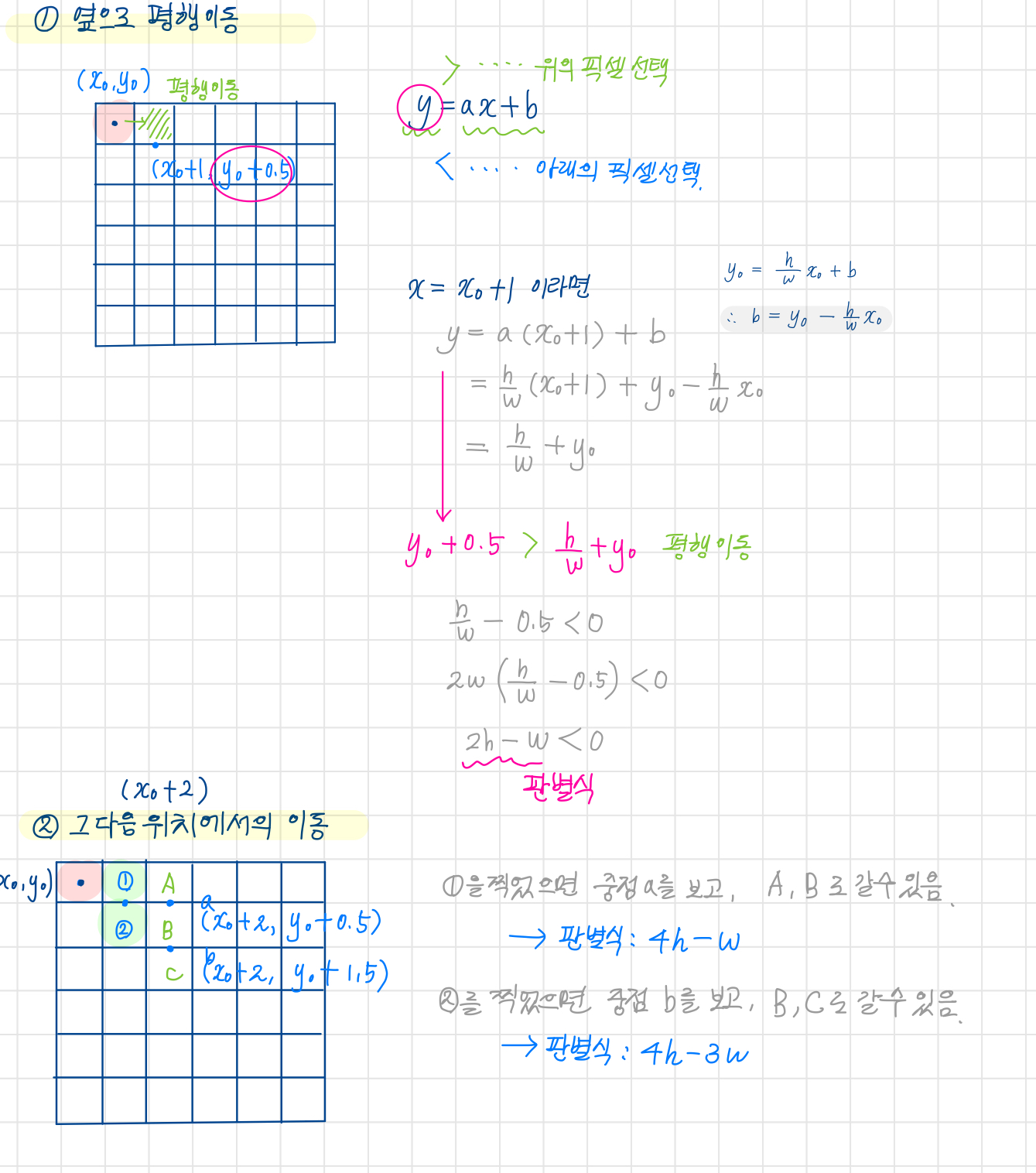

따라서 x가 증가할 때마다 판별 결과에 따라 판별식은 다음과 같이 변화된다고 할 수 있다.
- 평행 이동할 때는 2h만큼 증가
- 아래로 내려갈 때는 2h - 2w만큼 증가
이를 순서도로 표현하면 다음과 같다.
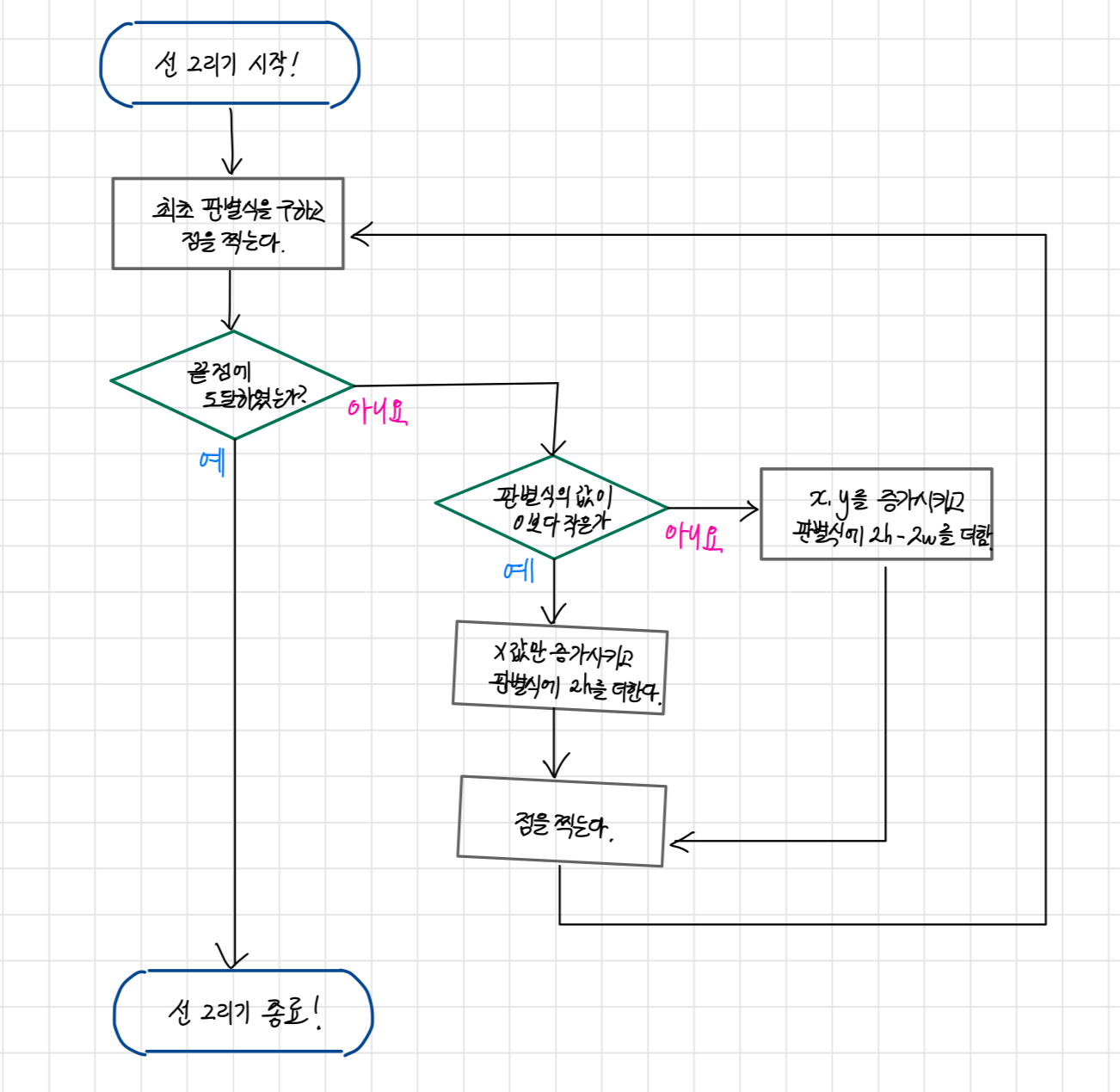
나머지 팔분면의 처리
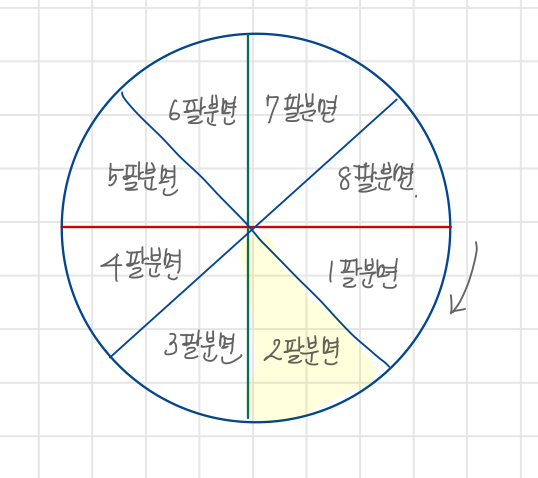
제 2팔분면은 x가 증가하지 않고 y를 증가시키는 방향으로 전개된다.
x와 y가 바뀐 상태로 동일하게 알고리즘을 진행하면 되며, 판별식은 2w-h가 된다.
3팔분면은 2팔분면에서 x를 거꾸로 증가시키는 형태이고
4팔분면은 1팔분면에서 x방향이 반대로 진행되는 것 외에는 동일하다.
이전의 알고리즘에서 앞에 다음과 같은 요소를 고려해 보완하면 모든 팔분면의 처리가 가능하다.
- 경사가 완만한가 급격한가?
- x방향과 y방향은 양의 방향인가 음의 방향인가?
이걸 바탕으로 일반화된 알고리즘을 만들어 전개하면 된다.
'Game > 게임 수학' 카테고리의 다른 글
| 게임 콘텐츠의 제작 원리 2-4. 삼각형 (0) | 2025.03.04 |
|---|---|
| 게임 콘텐츠의 제작 원리 2-2. 내적 (0) | 2025.02.28 |
| 게임 콘텐츠의 제작 원리 2-1. 아핀공간 (0) | 2025.02.27 |
| 게임을 지탱하는 기초 수학 1-8. 역행렬 (0) | 2025.02.27 |
| 게임을 지탱하는 기초수학 1-7. 행렬 (0) | 2025.02.26 |





