Machineboy空
게임 콘텐츠의 제작 원리 2-1. 아핀공간 본문
1. 아핀 공간(Affine Space)
이동 변환의 문제점
왜 아핀 공간이 필요한가? 컴퓨터 그래픽스에서 이동 기능을 빼놓을 수 없는데
앞선 선형변환을 이용해 이동을 구현할 수 없다.
왜냐면 원점에서부터 시작하는 벡터의 특성상 기저벡터를 원점으로부터 분리해 이동시킬 수 없기 때문

즉 다음과 같은 행렬은 존재하지 않는다.

밀기 변환의 활용
하지만 밀기 변환을 살짝 변형하면 이동기능을 구현할 수 있다!
밀기 변환을 활용해 선형 변환의 형태로 이동을 구현하는 것이 가능하다.
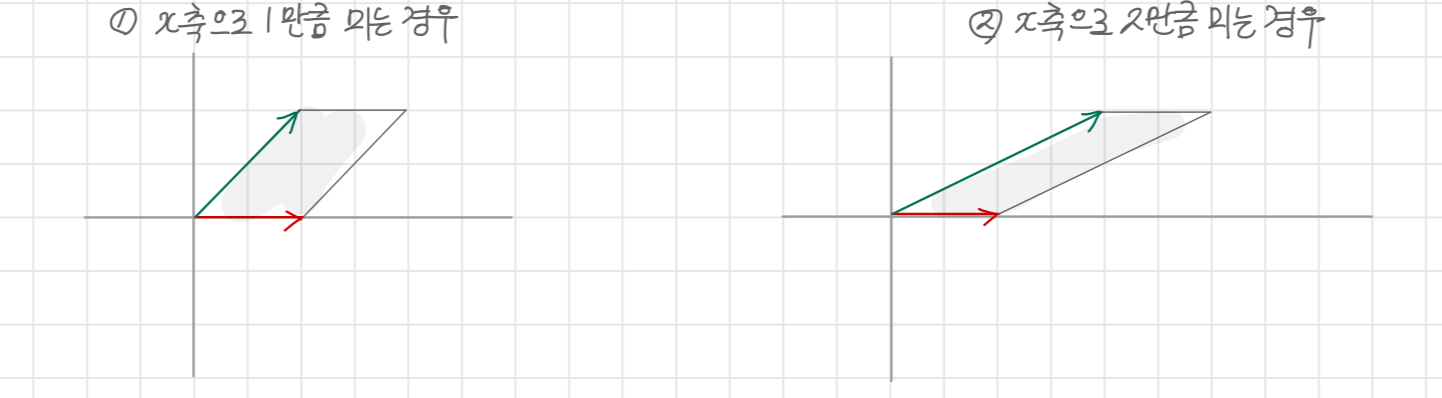

평면의 이동 변환
2차원의 밀기 변환을 통해 1차원의 이동을 구현했듯,
3차원의 공간에서 평면을 밀면 평면의 이동 구현이 가능해 진다!
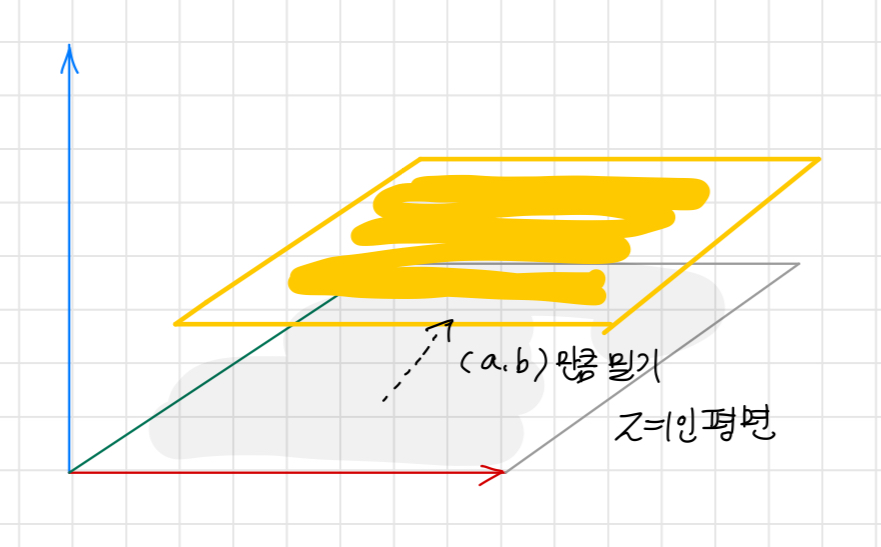
수식으로 나타내면 다음의 3차원 정방 행렬을 사용하면 원하는 만큼 2차원 평면의 이동 구현이 가능해진다.
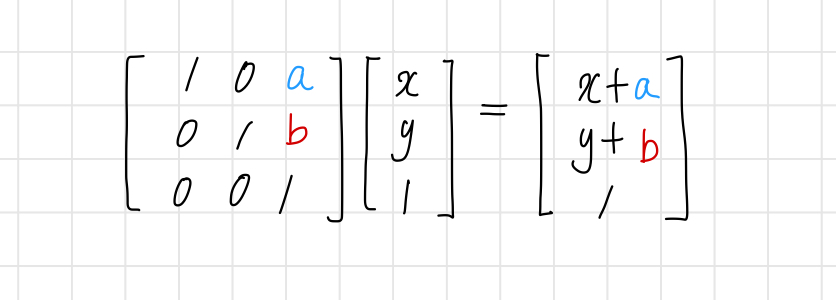
위와 같이 계산한 후 세 번째 요소는 버리면 이동 구현이 가능해진다.
아핀 변환(Affine transformation)
점을 만들어내는 새로운 이동 변환

다른 변환들도 여기에 맞춰서 한 차원을 높이면 행렬곱으로 크기, 회전, 이동을 구현한 것이 가능해진다.
마지막 차원의 z축은 아무것도 변하지 않게 1으로 고정.
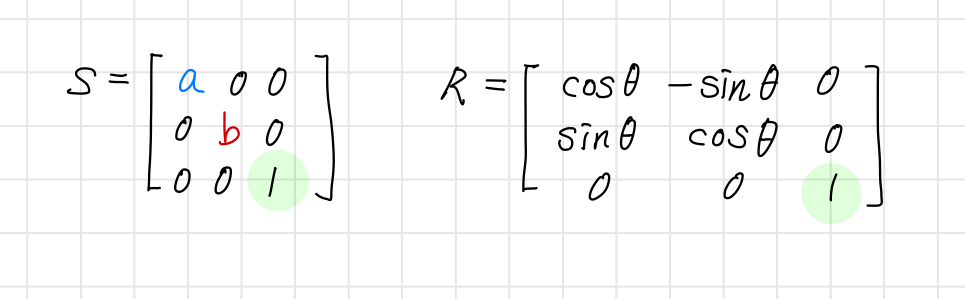
아래의 변환은 게임 제작에 필수적으로 사용되는 아핀 변환이다.
- 이동(Translation)
- 크기(Scale)
- 회전(Rotation)
아핀 공간의 요소(Affine Space Elements)
무대가 되는 벡터 공간에서 노란색을 구성하는 부분 공간을 아핀 공간A이라고 한다.
그리고 아핀 공간에 속한 원소를 따로 점(Point)라고 한다.

점은 마지막 차원 값이 1인 특별한 유형을 가진 벡터를 의미한다.
- 2차원 공간의 점: (x,y,1)
- 3차원 공간의 점: (x,y,z,1)
아핀 공간의 이동 벡터(변위 벡터)
점과 점의 대응 관계를 나타내기 위해서 사용하는 또 다른 종류의 벡터.
점에 이동벡터를 더하면 다른 벡터를 생성할 수 있다.

점은 마지막 차원의 값이 1이어야 하는데, 이동벡터를 더했을 때 변하면 안되기 때문에
이동벡터의 마지막 차원의 값은 0
- 2차원 공간의 이동 벡터: (x,y,0)
- 3차원 공간의 이동 벡터: (x,y,z,0)
이동 벡터의 마지막 차원 값은 0이기 때문에 점이 이동 벡터를 더하면 마지막 차원의 값은 언제나 1을 보장받는다.
아핀 공간의 구성 요소
- 점
- 물체의 시각적 표현을 위한 위치 정보
- 이동시킬 수 있는 대상
- 이동 벡터(벡터)
- 점을 이동시키는 무형의 매개체
- 같은 공간 내에서 이동시키는데 필요한 벡터

아핀 공간의 규칙
- 점 - 점 = 벡터 (마지막 차원 값 생각했을 때 1 - 1 = 0)
- 점 + 벡터 = 점 (마지막 차원 값 생각했을 때 1 + 0 = 1)
- 벡터 + 벡터 = 벡터 (마지막 차원 값 생각했을 때 0 + 0 = 0)
- 점 + 점 = 아핀 공간을 벗어나기 때문에 사용할 수 없다. (마지막 차원 값 생각했을 때 1 + 1 = 2)
이러한 규칙은 점에 대응되는 개념은 시각으로 벡터에 대응되는 개념은 시간으로 바꿔 설명할 수 있다.
- 점 - 점 = 시각 - 시각 : 3시 - 2시 = 1시간
- 점 + 벡터 = 시각 + 시간 : 3시 - 2시간 = 1시
- 벡터 + 벡터 = 시간 + 시간 : 3시간 - 2시간 = 5시간
- 점 + 점 = 시각 + 시각 : 3시 + 2시 = ??
아핀 공간의 의의
우리가 사용하는 게임이란 무대 공간 = 한 차원 높은 벡터 공간을 생성하고 이 안에서 아핀 공간을 활용해 이동을 구현할 수 있으며, 아핀 공간 위에서 캐릭터가 움직이고 탐험 가능한 월드 공간의 기반이 만들어지게 된다.
월드 공간 위에서 배치하는 물체는 아핀 공간의 점을 사용해 구성되고, 물체의 움직임은 이동 벡터를 활용해 구현한다.
앞서서 배운 수학적 개념의 벡터와 구분하기 위해 이동 벡터로 불렀지만 이 이동벡터는 바로 물리학에서 이야기하는 벡터의 개념과 동일하다.
게임 공간의 기초를 다졌다 이제.
'Game > 게임 수학' 카테고리의 다른 글
| 게임 콘텐츠의 제작 원리 2-3. 선 (0) | 2025.03.03 |
|---|---|
| 게임 콘텐츠의 제작 원리 2-2. 내적 (0) | 2025.02.28 |
| 게임을 지탱하는 기초 수학 1-8. 역행렬 (0) | 2025.02.27 |
| 게임을 지탱하는 기초수학 1-7. 행렬 (0) | 2025.02.26 |
| 게임을 지탱하는 게임 수학 1-6. 선형성 (0) | 2025.02.25 |




