Machineboy空
게임을 지탱하는 게임 수학 1-6. 선형성 본문
1. 선형성(Linearity)
선형성의 정의
다음 두 가지 조건을 만족하면 선형성을 지닌다고 말한다.

선형성을 만족하는 함수 찾기
둘다 같은 직선의 모양인데 f(x) = ax + b는 왜 선형성을 만족하지 않을까?
선형성이란 선의 형태를 의미하기보다, 순수하게 인자의 1차 비례 관계로 구성된 대응 관계를 의미한다.
f(x) = ax + b에서 b라는 불순물(?)이 들어갔기 때문에 순수한 1차 비례 관계가 깨져 선형성을 만족하지 못한다.


선형성의 해석

- 가산성(Additivity)의 성질
- 물과 기름을 섞어서 넣은 결과는 물과 기름을 분리해 넣은 결과와 동일하다.
- 다른 불순물이 존재하지 않는다.
- 1차 동차성(Homogeniety of 1 degree)의 성질
- 어떤 함수는 1차적으로 순수한 비례 관계를 가진다.
- 불순물이 존재하지 않고 2차 이상의 비례관계를 가지지 않는다.
2. 선형 사상(Linear Mapping)
그래픽적으로는 이러한 선형성을 변환에 많이 사용하곤 한다.
사상과 함수의 차이
- 함수(Function): 집합과 집합의 대응관계
- 사상(Mapping): 집합이 가지는 수학적 체계(공리)를 보존하면서 서로 대응하는 관계
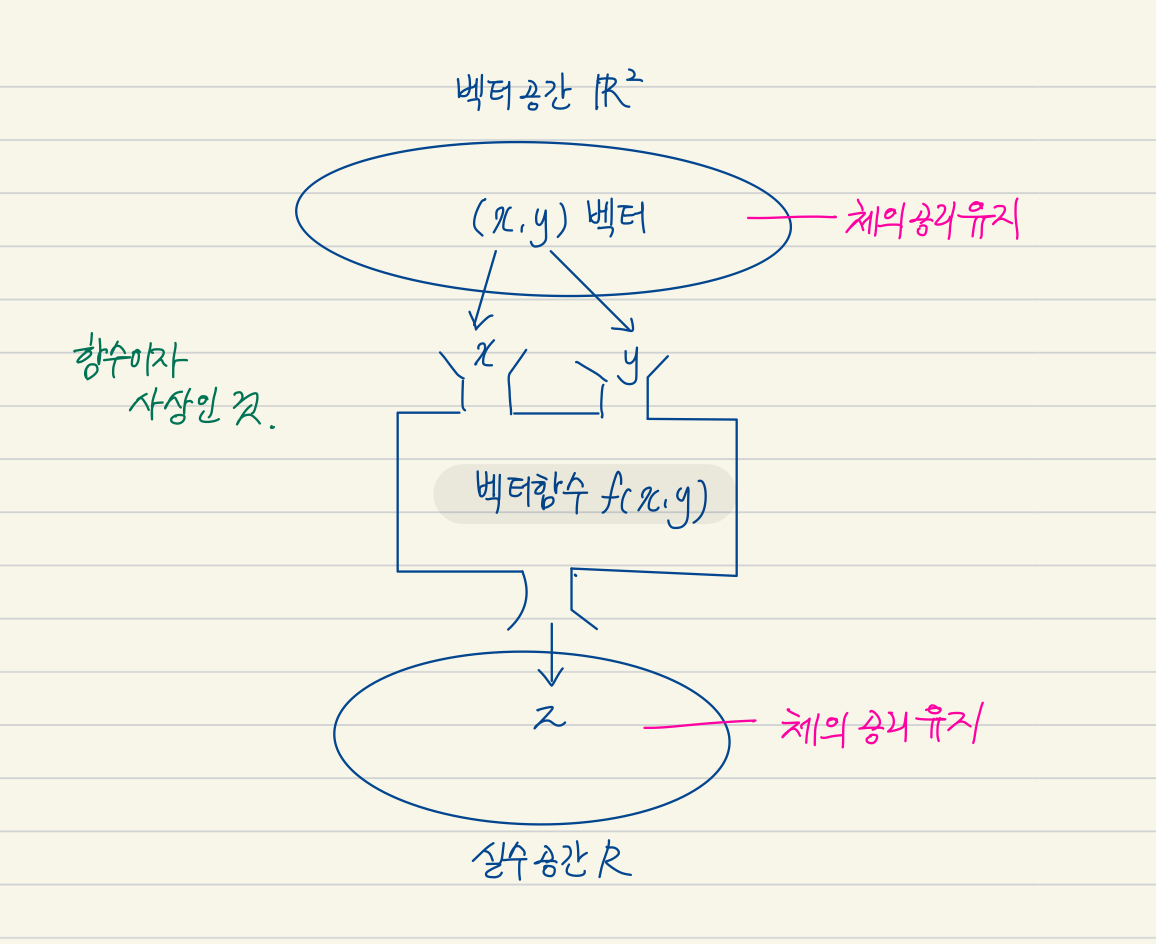
벡터 공간이 벡터 공간으로 대응된다는 것은 벡터의 공리를 그대로 유지함을 의미한다.
따라서 이는 넒은 관점에서 사상이라고 할 수 있다.
사상의 예
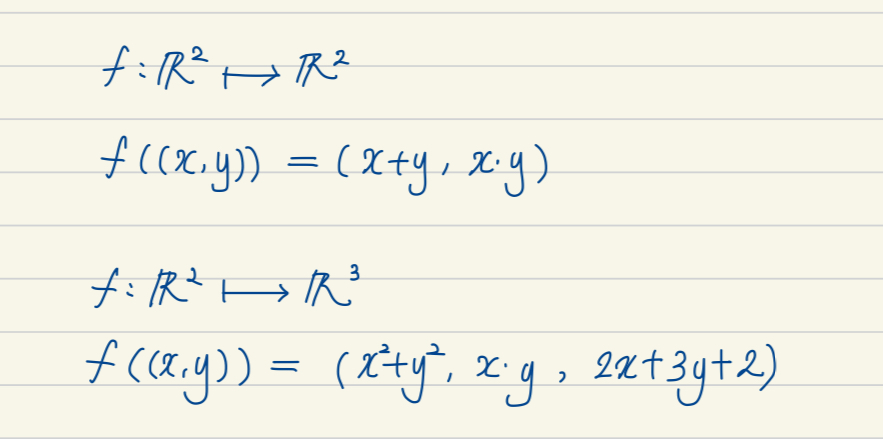
선형성을 가지는 사상의 조건

이를 만족하기 위해서는 불순물이 없는 순수한 1차적 대응 관계를 가져야 한다.
f((x,y)) = (ax + by, cx + dy)는 언제나 선형성을 만족하는지 확인해보자.


따라서 사상 f((x,y)) = (ax + by, cx + dy)는 언제나 선형성을 만족한다.
선형 사상과 선형 변환
- 선형 사상(Linear Mapping) = 선형성을 가진 두 구조의 대응관계
- 선형 변환(Linear Transformation) = 선형성을 가진 벡터 공간과 벡터 공간의 대응관계
벡터 공간에서는 선형 사상을 선형 변환(Linear Transformation)이라고도 하며 2차원 벡터 공간의 선형 변환은 다음의 형태를 가진다.

벡터 공간에 맞는 선형 변환이란 용어를 사용하겠다. 앞으로!
'Game > 게임 수학' 카테고리의 다른 글
| 게임을 지탱하는 기초 수학 1-8. 역행렬 (0) | 2025.02.27 |
|---|---|
| 게임을 지탱하는 기초수학 1-7. 행렬 (0) | 2025.02.26 |
| 게임을 지탱하는 기초 수학 1-5. 삼각함수 (0) | 2025.02.20 |
| 게임을 지탱하는 기초 수학 1-4. 선형 독립 (0) | 2025.02.19 |
| 1-2. 게임을 지탱하는 기초 수학 - 벡터 (0) | 2025.02.18 |




