Machineboy空
1-2. 게임을 지탱하는 기초 수학 - 벡터 본문
1. 벡터(Vector)의 정의
게임 시스템의 근간을 이루는 벡터.
수 직선에서의 표현의 한계
실수는 원소들의 집합이고 이걸 표현하기 위해 쭉 이어진 직선을 그렸었다.
시각적인 관점에서 수를 바라보자면, 직선 위에 점으로 밖에 표현할 수 없다.
시각적으로 무언가 의미가 있으려면 적어도 평면은 되어야 원하는 그림을 그릴 수 있을 텐데
수만 가지고는 표현하기가 어렵다.
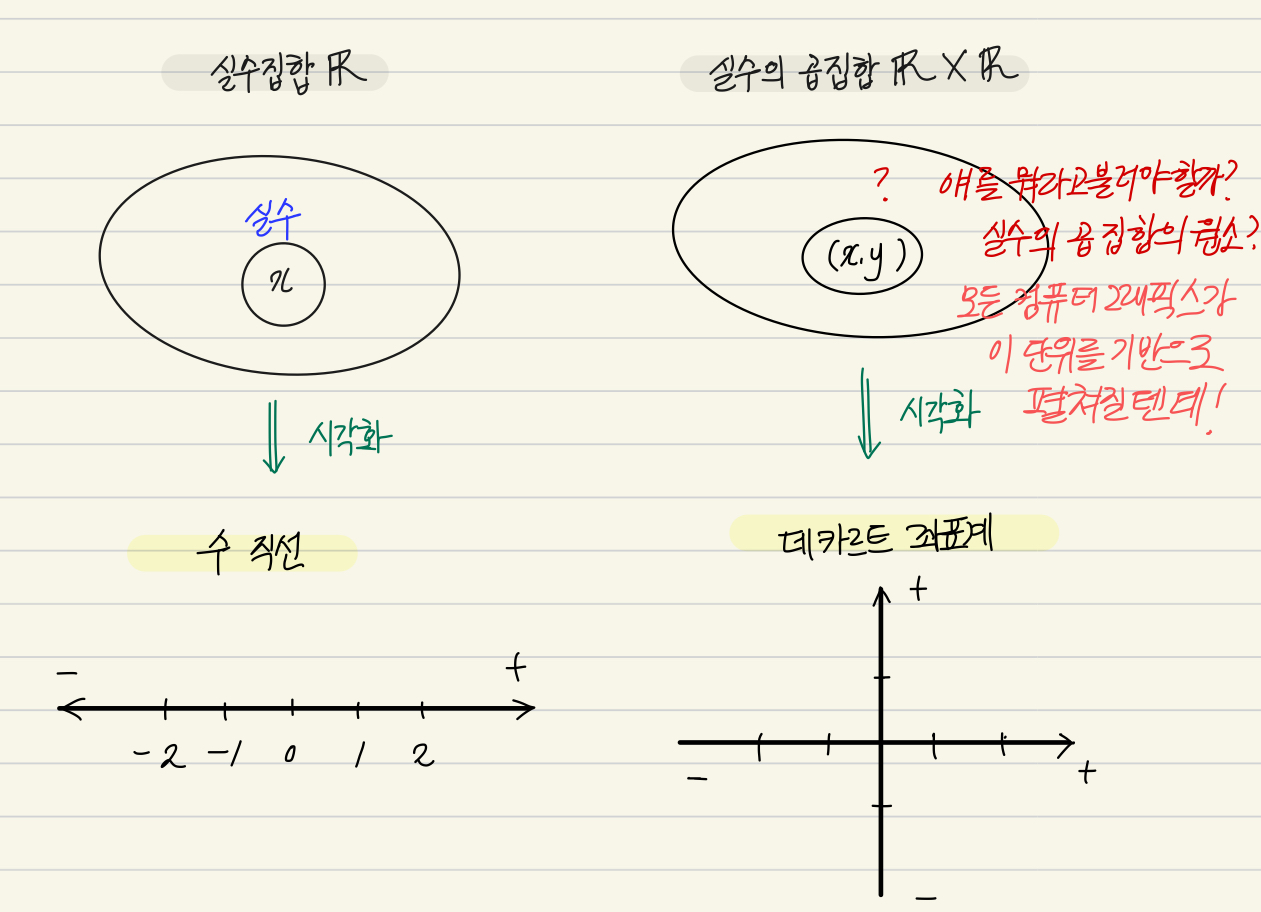
데카르트 좌표계(Cartesian Coordinate System)
수의 시스템을 기반으로 영역을 2차원으로 확장해 표현하는 방식.
두 실수의 집합을 교차시켜서 평면을 표현하고 오른쪽과 위쪽을 +방향으로 지정한다.

두 실수의 집합을 곱집합으로 확장한 R X R 로 볼 수 있다.
곱집합의 원소는 순서쌍이므로 두 집합의 원소를 각각 미지수 x와 y로 두면 이는 (x,y)로 표현할 수 있고, 이를 좌표(coordinate)라고 한다.
2차원 평면의 시각화
좌표에 해당하는 대상을 점으로 표현하면 다음과 같다.
- 점으로 표현
- 원점으로 부터 해당 점으로 뻗어나가는 화살표
벡터(Vector)와 벡터 공간(Vector Space)
- 수 - 벡터(Vector) - 스칼라들의 순서쌍
- 수집합 - 벡터 공간(Vector Space) - 벡터의 집합

실수의 집합을 체 집합으로 넓혀 생각한 것 처럼, 실수의 곱 집합도 체 집합의 곱으로 이해하고,
체 집합의 원소, 스칼라들이 이루는 순서쌍을 원소로 하는 집합을 벡터 공간이라고 이해해라.
2. 벡터의 연산(Vector Operations)
벡터 공간을 이용해서 다른 공간들을 만들어내려면, (= 벡터 공간이 변환되기 위해서는)
수의 이항 연산 처럼 벡터에도 연산이 필요하다.
벡터(Vector)의 기본 연산
1. 벡터와 벡터의 덧셈

- 1번 컵: 물 10ml + 기름 20ml
- 2번 컵: 물 30ml + 기름 10ml
둘을 합치면 물 40ml , 기름 30ml 인 용액이 된다.
물과 기름이 서로 섞이지 않는 것 처럼, 두 실수 집합이 직교한다는 것은 서로 독립적으로 동작함을 의미한다.
2. 벡터와 스칼라의 곱셈

두 연산을 시각적인 관점에서 바라본다면!
| 벡터와 벡터의 덧셈 | 벡터와 스칼라의 곱셈 |
| x만큼 평행이동, y만큼 평행이동 | 같은 기울기를 가지는 무한대의 선 위에서 이동 |
외적이나 내적은 응용편
벡터의 크기(Norm)
- 수의 크기 = 원점으로부터의 거리 | x |
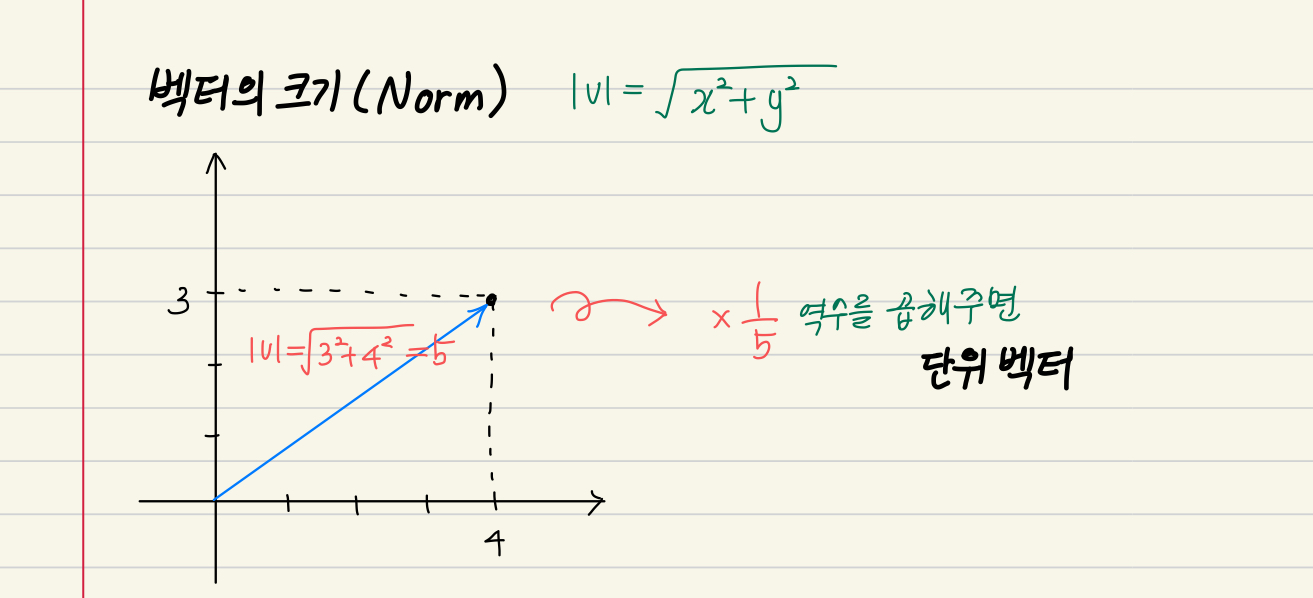
- 벡터의 크기(Norm) = 원점으로부터의 최단 거리 | v |
- 단위 벡터 : 크기가 1인 벡터
- 벡터의 크기의 역수를 곱하면 단위 벡터가 만들어 진다.
3. 벡터 공간의 공리
벡터 공간의 시스템은 수를 시스템적인 측면에서 분석한 체(Field)의 시스템을 기반으로 확장해 만든 시스템으로 볼 수 있으며, 이는 8개의 공리로 구성되어 있다.
u,v,w는 벡터를 의미하고, a,b는 스칼라를 의미한다.

실 벡터 공간(Real Vector Space)
벡터 공간의 기반을 이루는 체 집합으로 구체적으로 실수 집합 R을 사용하기로 했다면,
그것을 실 벡터 공간이라고 한다.
그리고 앞으로 실 벡터 공간을 사용해 컴퓨터 그래픽을 구현할 것이다.
'Game > 게임 수학' 카테고리의 다른 글
| 게임을 지탱하는 기초 수학 1-5. 삼각함수 (0) | 2025.02.20 |
|---|---|
| 게임을 지탱하는 기초 수학 1-4. 선형 독립 (0) | 2025.02.19 |
| 1-2. 게임을 지탱하는 기초 수학 - 함수 (0) | 2025.02.18 |
| 1-1. 게임을 지탱하는 기초 수학 - 수의 구조 (0) | 2025.02.17 |
| Vector 연산 기초 (1) | 2024.09.30 |




