Machineboy空
1-2. 게임을 지탱하는 기초 수학 - 함수 본문
1. 함수(Function)의 기초
함수를 왜 배워야 하는가?
게임을 만든다는 것은 대부분 공간과 공간의 변환으로 구성되어 있다.
이러한 변환은 근본적으로 집합과 집합의 대응 관계에 기반하고 있으며, 이 과정은 함수로 설명된다.
함수의 정의
X와 Y 두 집합의 대응관계를 의미.

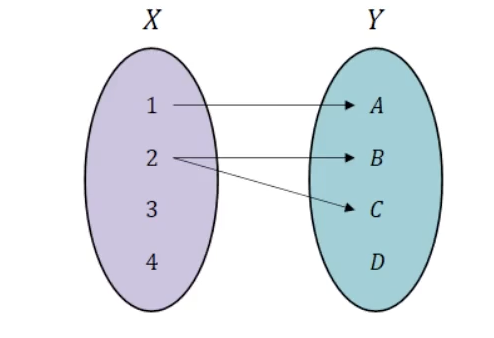
함수의 성립 조건: 첫 번째 집합의 모든 요소가 사용되어야 한다.
함수가 아닌 대응 관계
- 첫번째 집합의 어떤 원소에 대한 대응 관계가 빠져 있을 때
- 첫번째 집합의 한 원소가 두 번째 집합의 두 가지 이상 원소에 대응할 때
함수에 관련된 주요 용어
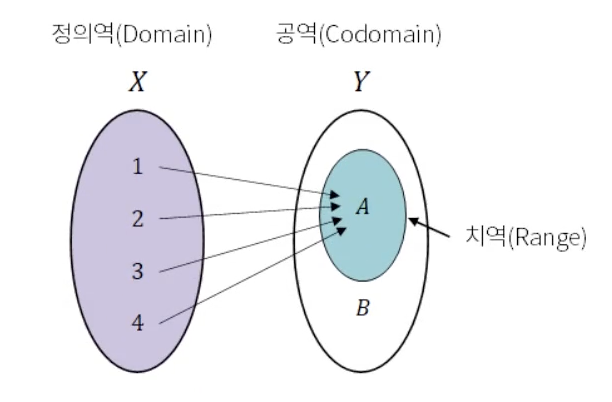
- 정의역 (Domain)
- 공역 (Codomain)
- 치역 (Range) : 공역의 모든 원소에 대응되는 것은 아니므로 대응되는 요소만을 모아 치역이라고 함.

프로그래밍 관점에서의 함수
- 입력(Input) : '정의역'
- 출력(Output) : '공역'
함수의 종류(Classes of Function)
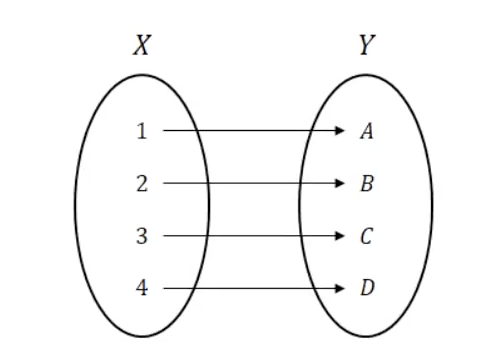
- 전사(Subjection) : 공역과 치역이 동일
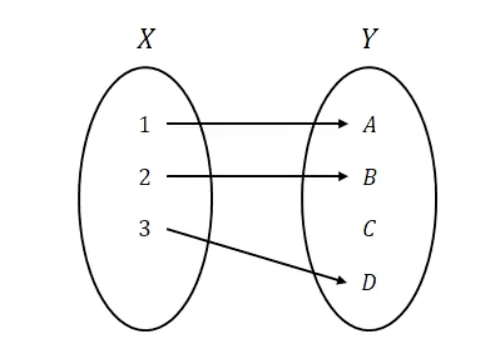
- 단사(Injection) : 정의역과 공역의 요소가 1:1로 대응
- 전단사(Bijection) : 전사 + 단사를 모두 만족
- 일반(General): 이도 저도 아닌 것

2. 곱집합 (Cartesian Product)
곱집합(AXB)의 정의
곱집합이란 두 집합의 원소를 순서쌍으로 묶어 구성한 집합.
(a,b)와 같이 원소를 나열하는 방식을 Tuple이라고 한다.
곱집합은 X 기호를 사용해 표현한다.
a는 A로 부터 온 것, b는 B로 부터 온 것으로 두 집합을 합친 것이라 이해할 수 있다.


- 집합 R = {A,K,Q,J,10,9,8,7,6,5,4,3,2}
- 집합 S = {♠,♣,♥,⬥}
- 트럼프 카드 : R X S
뿐만 아니라 좌표 계산에서도 곱집합 개념이 사용될 것.
이항 연산을 함수로 해석하기
지금까지는 하나의 입력을 넣어 출력을 만드는 함수를 살펴봤는데,
이항 연산은 2개의 입력을 넣어야 한다. 즉 곱집합을 정의역에 넣으면 이항 연산을 만들어내는 함수 시스템 구축 가능.

3. 합성함수(Composition)
두 함수를 두 단계를 거쳐 수행하는 것이 아니라, 한 단계로 합쳐 수행하는 것.
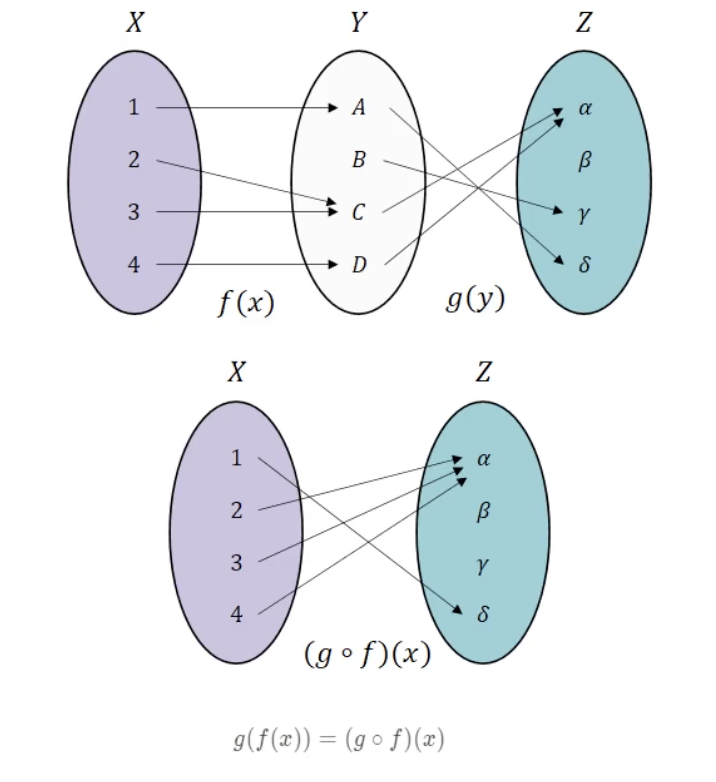
함수의 대응관계
- 항등함수(Identity Function) : 똑같은 원소가 대응되는 관계 (기호 i)
- 역함수(Inverse Function) : 역원 처럼, 출력값이 자기 자신을 만들어주는 함수
- 역함수의 조건
- 전사, 단사 함수들은 역함수가 성립되지 않는다.
- 전단사인 경우에만 역함수가 성립한다.
- 역함수의 조건

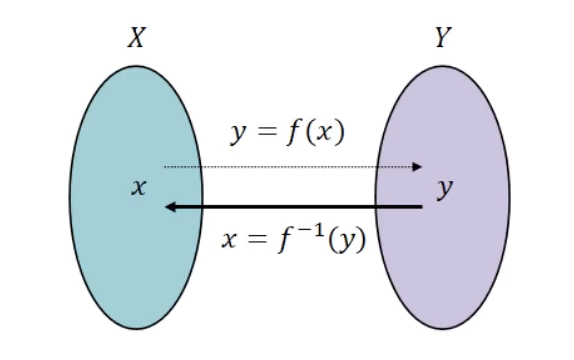

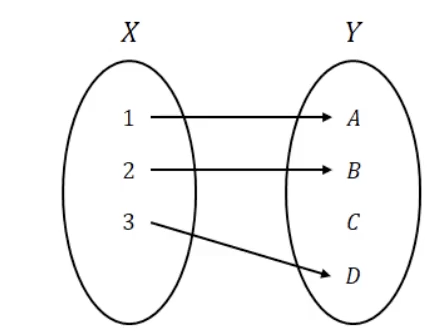
함수와 그 역함수의 합성함수
항등함수가 된다.
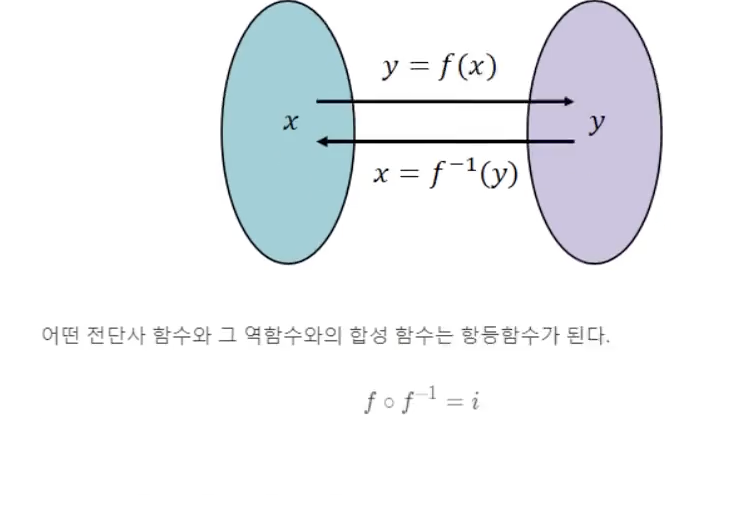
합성함수의 역함수
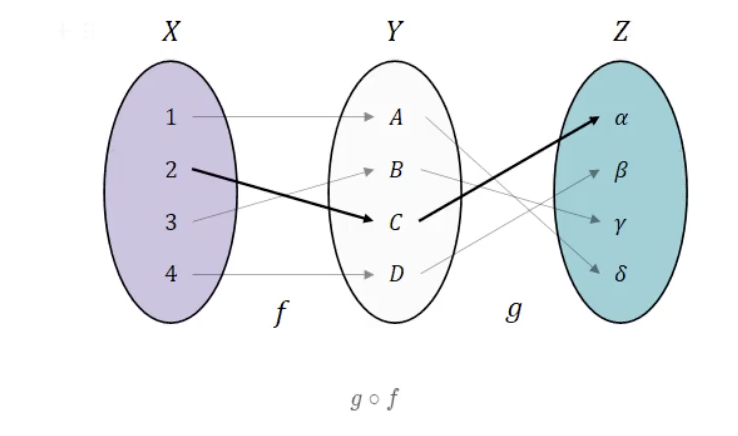

왜 이러한 합성함수의 대응관계를 알아야 하는가?
이후에 배울 행렬은 하나의 함수에 대응이 되고, 행렬의 곱셈은 합성 함수에 대응된다.
합성 함수의 성질을 이해하면 복잡한 행렬 연산의 매커니즘을 이해하는 기반이 된다.
'Game > 게임 수학' 카테고리의 다른 글
| 게임을 지탱하는 기초 수학 1-4. 선형 독립 (0) | 2025.02.19 |
|---|---|
| 1-2. 게임을 지탱하는 기초 수학 - 벡터 (0) | 2025.02.18 |
| 1-1. 게임을 지탱하는 기초 수학 - 수의 구조 (0) | 2025.02.17 |
| Vector 연산 기초 (1) | 2024.09.30 |
| 오른손 좌표계와 왼손 좌표계 (0) | 2024.06.23 |




