Machineboy空
게임을 지탱하는 기초 수학 1-8. 역행렬 본문
1. 역행렬(Inverse Matrix)
행렬은 큰 관점에서 선형변환을 시키는 함수의 개념이기 때문에 역행렬도 역함수에 대응해 생각할 수 있다.
항등 행렬(Identity Matrix)
* 항등 함수 = 정의역과 치역의 결과물이 같은 것
선형 변환의 결과가 변함없는 행렬.
두 표준 기저벡터 e1, e2의 값이 동일하게 유지되는 선형 변환을 의미한다.

역행렬이란?
선형 변환된 결과를 거꾸로 돌려주는 선형 변환. 이를 합성한 결과는 항등 변환이 된다.

2. 역행렬의 계산 방법
행렬식(Determinant)
아래 연립방정식의 해는 존재하지 않는다.
ad-bc = 0이 되고, 이는 해가 없음을 의미한다. 어째서인가?

위 변환을 분석하면 표준기저벡터 e1, e2는 각각(2,1),(1,0.5)로 변환되었는데,
이 둘은 같은 기울기를 가지고 있음을 알 수 있다. 따라서 두 기저 벡터가 선형 독립에서 선형 의존 관계가 되었다.
이를 그림으로 나타내면 다음과 같다.

위의 경우 선형 변환의 결과로 2차원 평면이 1차원 직선으로 소멸되었기에
1차원에서 2차원으로 돌아가는 역행렬은 존재하지 않는다.
그렇다면 어째서 ad-bc 가 0이면 차원이 소멸되는 것인가?
두 벡터가 만드는 평행사변형의 넓이를 확인해보자.

만약 역행렬이 존재한다면 어떻게 되는가?
다음과 같은 변환을 생각하면 평면이 행려릭 값만큼 달라짐을 알 수 있다.
그렇다면 원상 복구하기 위해서는 달라진 크기의 역수만큼 변해야 한다.

역행렬의 활용
연립방정식의 해를 구할 때 유용하게 사용된다.
아래 식에서 선형 변환 A와 변형된 벡터 v'만 알고 있는 경우
A의 역행렬을 구할 수 있다면 양변에 곱해 변환되기 전의 벡터 v를 구할 수 있다.
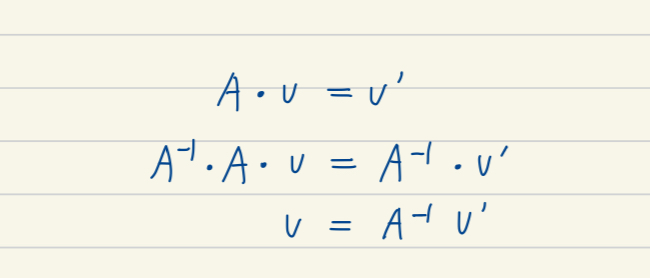
임의의 정방행렬의 역행렬을 구하기 위한 방법은 여러가지가 있는데 대표적으로 다음의 방법들이 존재한다.
- 가우스 소거법(Gaussian elimination)
- 크라메르 공식(Cramer's rule)
하지만 우리가 사용하는 대표적인 선형 변환들은 위의 방법을 사용하지 않고
직관적으로 역행렬을 구하는 것이 가능하다.
크기 행렬의 역행렬

밀기 행렬의 역행렬

회전 행렬의 역행렬

위 결과에서 Rθ 와 R(-θ)는 서로 전치 관계를 이룬다.
따라서 회전 행렬과 역행렬은 전치행렬이 됨을 알 수 있다.

'Game > 게임 수학' 카테고리의 다른 글
| 게임 콘텐츠의 제작 원리 2-2. 내적 (0) | 2025.02.28 |
|---|---|
| 게임 콘텐츠의 제작 원리 2-1. 아핀공간 (0) | 2025.02.27 |
| 게임을 지탱하는 기초수학 1-7. 행렬 (0) | 2025.02.26 |
| 게임을 지탱하는 게임 수학 1-6. 선형성 (0) | 2025.02.25 |
| 게임을 지탱하는 기초 수학 1-5. 삼각함수 (0) | 2025.02.20 |




