Machineboy空
게임 콘텐츠의 제작 원리 2-4. 삼각형 본문
1. 세 점의 아핀 조합(Affine combination of Three points)
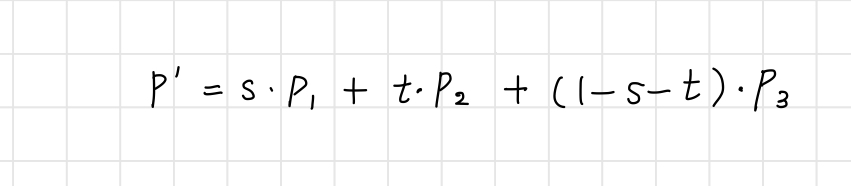
세 점의 아핀 조합으로 만들 수 있는 공간의 형태는?
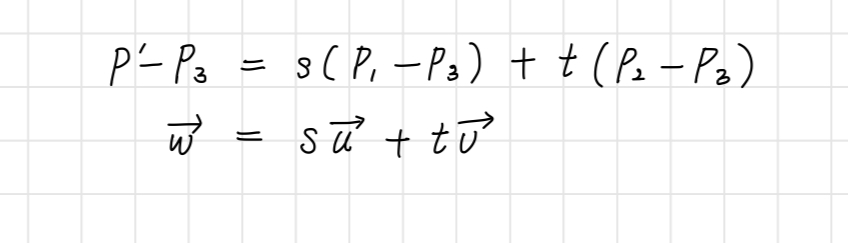
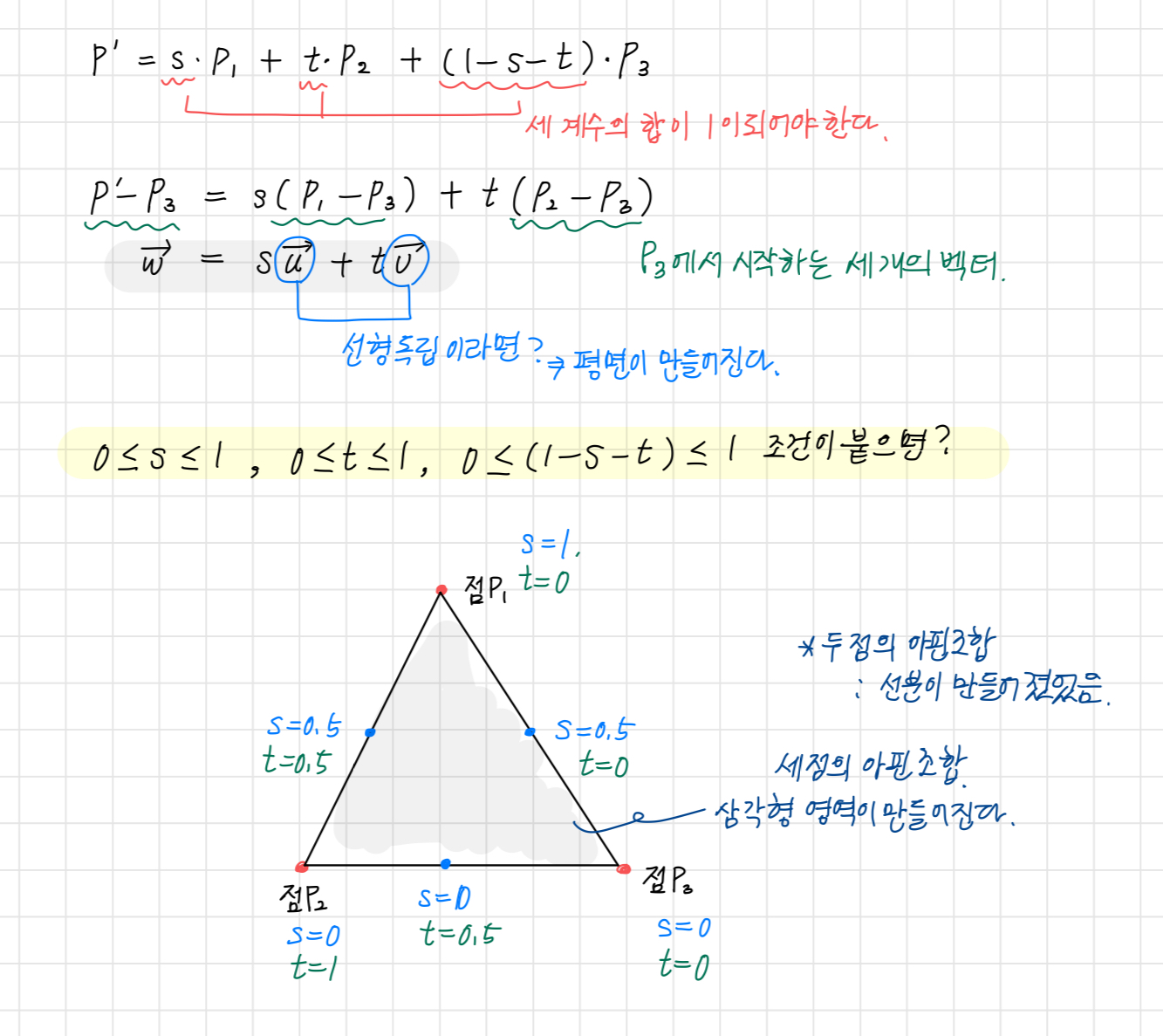
컨벡스 조합(Convex Combination)
아핀 조합에서 모든 계수의 크기가 0보다 크고 1보다 작은 경우를 컨벡스 조합이라고 한다.

컨벡스 조합을 통해 실제로 사용할 수 있는 형상이 완성된다.

볼록(Convex)과 오목 (Concave)
임의의 두 점이 연결한 선이 영역을 벗어나면 오목하다고 표현한다.
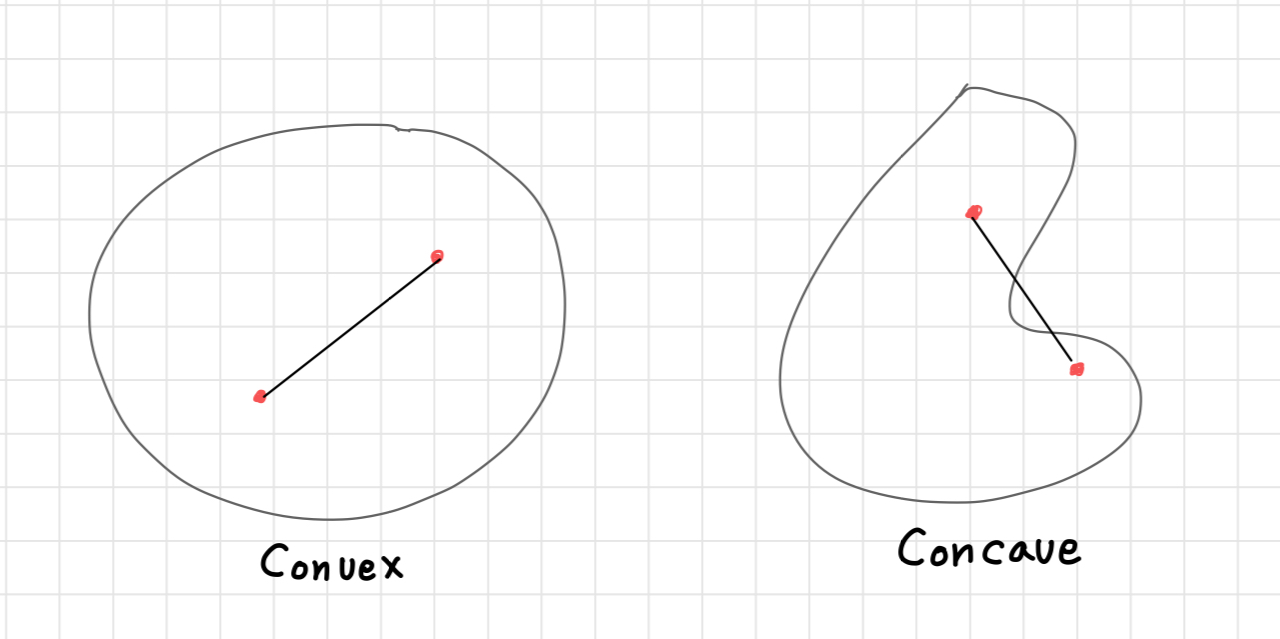
볼록함(Convexity)
영역 내 임의의 점을 연결한 선이 영역을 벗어나지 않는 성질

물리엔진에서의 MeshCollider에 나오는 Convex가 이것임.
볼록한 영역들이 충돌 계산할때 단순하고 빠르게 계산할 수 있게 도와줌
네 점의 컨벡스 조합
네 점의 컨벡스 조합은 조합에서 만들어지는 각 벡터가 선형 독립인 경우 다음과 같은 사면체가 나온다.

2. 메시(Mesh) 구조
이제부터 컨벡스한 도형을 사용해서 현실과 유사한 3차원에서의 물체를 만들 것.
선분, 삼각형, 사면체 중에서 가장 유용한 것은 삼각형
수학으로 만들어지는 컨벡스 영역 중에서 가장 효과적으로 사용할 수 있는 도형은 삼각형이다.
- 2차원 영역의 표현 가능
- 3차원은 2차원 표면을 조합해 표현 가능
3차원의 입체를 표현하는 것이지, 그 내부까지 보여주는 것이 아님.
게임 그래픽에서는 빨리 계산해서 처리해야하기 때문에 내용물보다 겉 표면만 그린다.
3차원 물체는 삼각형을 조합해 다음과 같이 생성된다.

이 삼각형들을 저장한 것을 Mesh 구조라고 한다.
메시(Mesh) 구조
- 정점과 삼각형 정보를 별도로 구성하는 삼각형 리스트(Triangle List) 방식을 사용한다.
정점 버퍼에는 정점을 모아두고 인덱스 버퍼에는 삼각형 정보를 모아둔다.
삼각형 두 개로 구성되는 사각형은 다음과 같이 설계할 수 있다.
이때 두 삼각형이 겹치는 정점은 재활용해 배치가 가능하다.

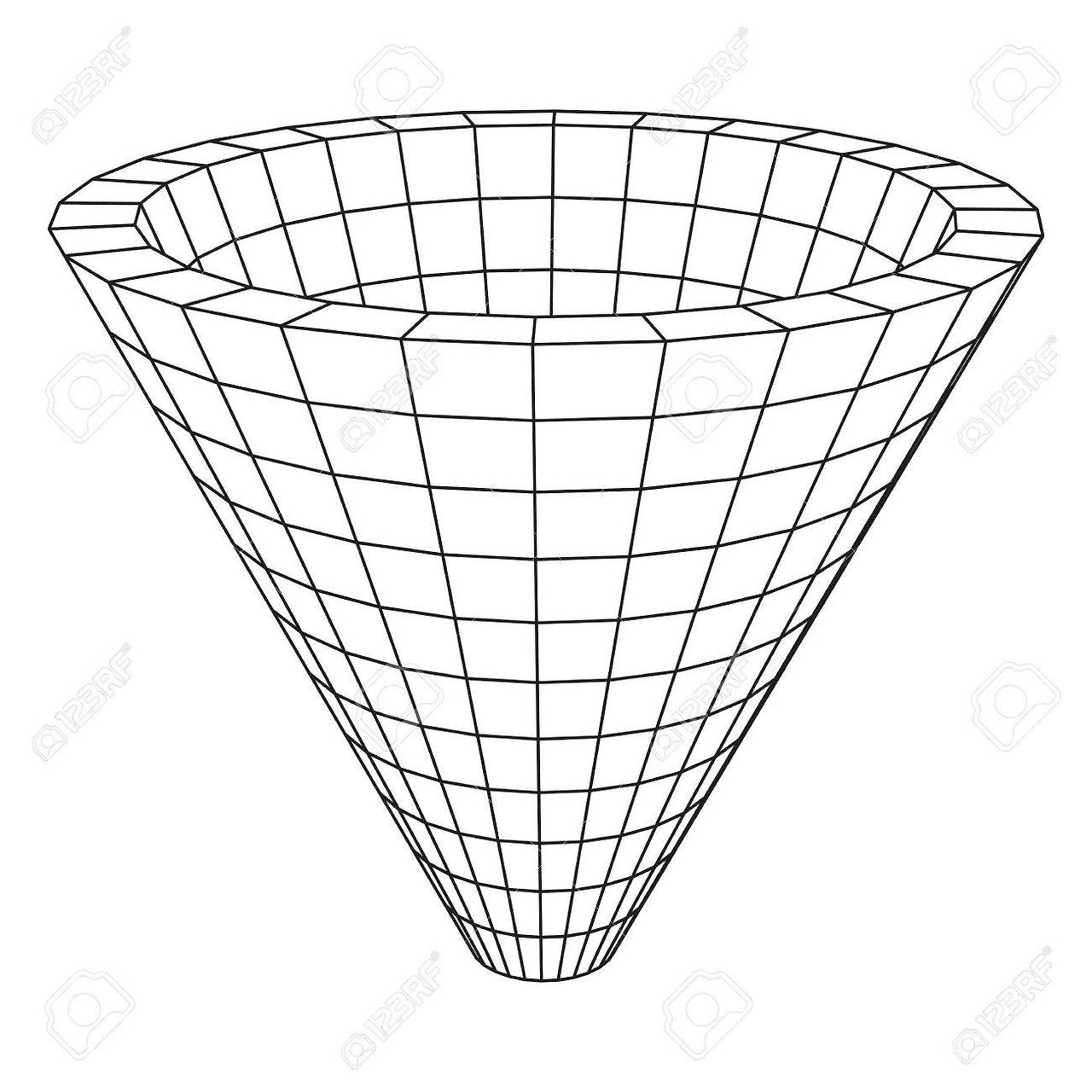
와이어프레임(Wireframe)
삼각형마다 점을 연결해 선 그려 메시를 형상화한 결과 화면
3. 무게중심좌표(Barycentric Coordinate)
메쉬를 다룰 때 중요하게 알아야 하는 개념
다음과 같은 아핀 조합의 식에서
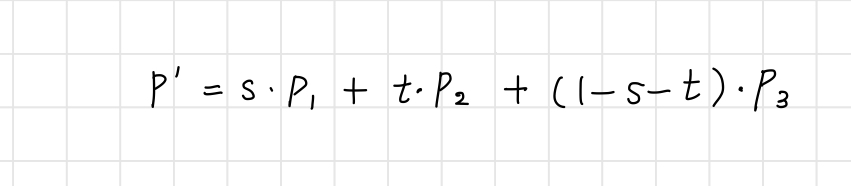
세 계수를 조합해 (s, t, 1-s-t)생성한 좌표를 무게중심좌표라고 한다.
무게 중심 좌표의 계산방법

무게 중심 좌표의 활용 - 삼각형 채우기

이 중에서 컨벡스 조건을 만족하는 픽셀만 그린 결과 화면
'Game > 게임 수학' 카테고리의 다른 글
| 게임 콘텐츠의 제작 원리 2-6. 게임 엔진 (0) | 2025.11.27 |
|---|---|
| 게임 콘텐츠의 제작 원리 2-5. 텍스쳐매핑 (0) | 2025.11.27 |
| 게임 콘텐츠의 제작 원리 2-3. 선 (0) | 2025.03.03 |
| 게임 콘텐츠의 제작 원리 2-2. 내적 (0) | 2025.02.28 |
| 게임 콘텐츠의 제작 원리 2-1. 아핀공간 (0) | 2025.02.27 |




