Machineboy空
인접행렬(adjacneny matrix) 와 인접리스트 (adjacency list) 본문
https://blog.naver.com/jhc9639/222289089015
[알고리즘 강의] 2주차. 그래프이론, 인접행렬, 인접리스트, DFS, BFS, 트리순회
이번주차는 그래프이론과 DFS(깊이우선탐색), BFS(너비우선탐색) 그리고 트리순회인 preorder, inord...
blog.naver.com
인접해있다 = 연결되어있다.
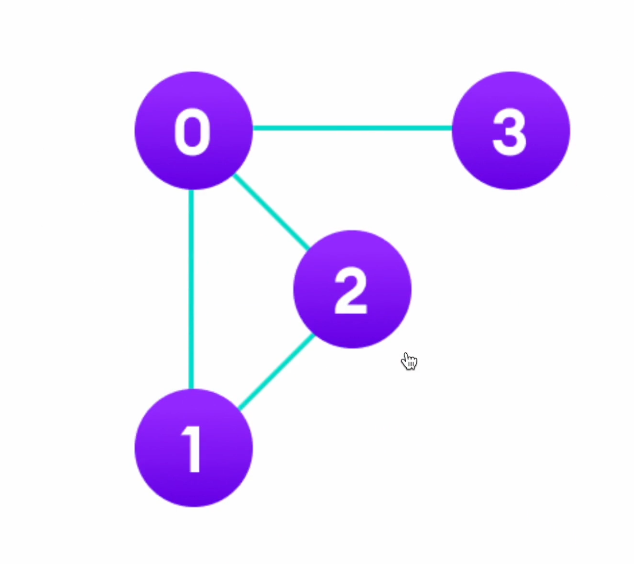

화살표가 없는 간선을 무방향 간선이라고 한다.
즉, 무방향 간선이 양방향 간선이다.
인접 행렬(adjacneny matrix)
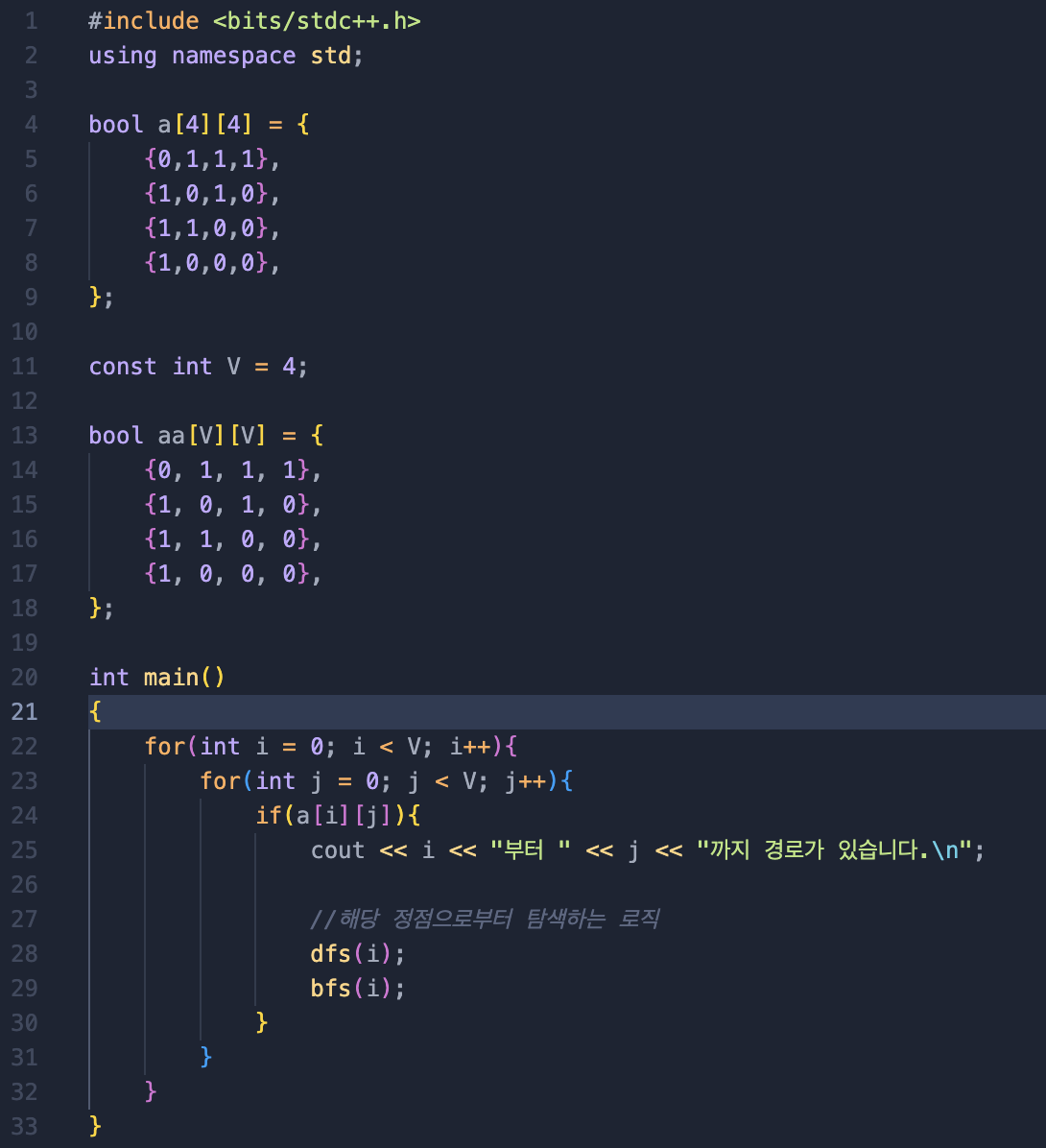
인접행렬이란 그래프에서 정점과 간선의 관계를 나타내는 bool 타입의 정사각형 행렬을 의미한다.
0은 두 정점 사이의 경로가 없음, 1은 두 정점 사이의 경로가 있음.
a[from][to]
i 부터 j 까지는 경로가 있습니다. 느낌으로 사용하는 거.
그렇다면 2차원 행렬을 탐색하는 코드를 구현할 때
- y축 기준으로 행 묶음으로 탐색
- x축 기준으로 열 묶음으로 탐색

y축 기준 행 탐색을 하도록 하자.
c++에서는 행 기준으로 탐색해서 더 빠르다고 함
예제들
Q. 3번 노드에서 5번 노드로 가는 단방향 경로가 있고 이를 인접행렬로 표현한다면 어떻게 될까?
a[3][5] = 1;
Q. 3번 노드에서 5번 노드로 가는 양방향 경로가 있고 이를 인접행렬로 표현한다면 어떻게 될까?
a[3][5] =1;
a[5][3] =1;
Q. 정점의 갯수가 20개인 그래프가 있다. 이를 인접행렬로 표현한다고 했을 떄 메모리를 최소로 쓴다고 하면 배열을 어떻게 만들어야 할까?
bool a[20][20];
Q. 인접행렬 기반 탐색
- 정점은 0번 ~ 9번까지 10개
- 1-2/1-3/3-4라는 경로가 있다.
- 0번부터 방문하지 않은 노드를 찾고 해당 노드부터 방문, 연결된 노드를 이어서 방문해서 출력하는 재귀함수를 만들고 싶다면 어떻게 해야할까?
#include <bits/stdc++.h>
using namespace std;
const int V = 10;
bool a[V][V], visited[V];
//방문했다면 넘어가고,
//방문하지 않았다면, 연결된지 확인 후 방문하도록!
void go(int from)
{
visited[from] = 1;
cout << from << '\n';
for (int i = 0; i < V; i++)
{
if (visited[i])
continue;
if (a[from][i])
{
go(i);
}
}
return;
}
int main()
{
// 양방향 간선
a[1][2] = 1; a[1][3] = 1; a[3][4] = 1;
a[2][1] = 1; a[3][1] = 1; a[4][3] = 1;
for(int i = 0; i<V; i++){
for(int j = 0; j < V; j++){
if(a[i][j]&& visited[i] == 0){
go(i);
}
}
}
}인접리스트(adjacency list)
2차원 배열로 나타내는 것이 아니라 연결 리스트를 여러 개 만들어 그래프를 표현하는 방법
연결된 정점을 배열에 넣음

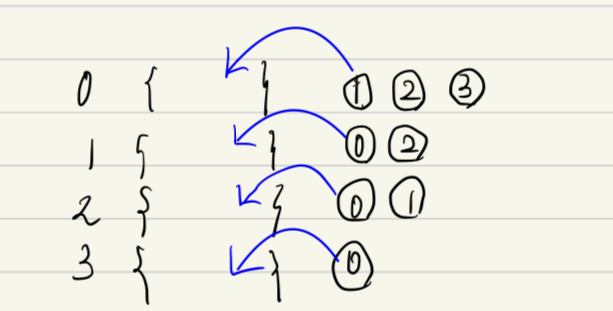
#include <bits/stdc++.h>
using namespace std;
const int V = 4;
vector<int> adj[V]; // list가 아닌 vector로도 구현할 수 있다. 편의상 vector로 구현하겠음
//정점마다 연결리스트가 필요하니까, 4개의 벡터가 있는 것.
int main(){
adj[0].push_back(1);
adj[0].push_back(2);
adj[0].push_back(3);
adj[1].push_back(0);
adj[1].push_back(2);
adj[2].push_back(0);
adj[2].push_back(1);
for(int i = 0; i < 4; i++){
cout << i << " :: ";
for(int there : adj[i]){
cout << there << " ";
}
cout << '\n';
}
}
왜 인접리스트가 아닌 vector도 되는 것일까?

| 연결리스트 | vector | ||
| n번째 인덱스에 삽입,삭제 | O(1) | n번째 인덱스에 삽입,삭제 | O(n) |
| 마지막 요소에 삽입,삭제 | O(1) | 마지막 요소에 삽입,삭제 | O(1) |
| 특정요소 탐색 (순차적 탐색만 가능) |
O(n) | 특정요소 탐색 | O(n) |
| n번째 요소 참조 | O(n) | n번째 요소 참조 | O(1) |
인접리스트를 구현할 때 많이 사용되는 연산은 마지막 요소에 삽입과 해당 배열을 탐색하는 연산.
그래서 vector로 구현해도 무방
예제
Q. 인접리스트를 기반으로 탐색하기
- 정점은 0번 ~ 9번까지 10개
- 1-2/1-3/3-4라는 경로가 있다.
- 0번부터 방문하지 않은 노드를 찾고 해당 노드부터 방문, 연결된 노드를 이어서 방문해서 출력하는 재귀함수를 만들고 싶다면 어떻게 해야할까?
#include <bits/stdc++.h>
using namespace std;
const int V = 10;
vector<int> adj[V];
int visited[V];
void go(int idx){
cout << idx << '\n';
visited[idx] = 1;
for(int there: adj[idx]){
if(visited[there]) continue;
go(there);
}
return;
}
int main(){
adj[1].push_back(2);
adj[1].push_back(2);
adj[1].push_back(2);
adj[1].push_back(2);
adj[1].push_back(2);
adj[1].push_back(2);
for(int i = 0; i < V; i++){
if(adj[i].size() && visited[i]==0) go(i);
}
}인접행렬과 인접리스트의 차이 (외우기)
둘 중에 어떤 것을 써야 할까?
V(vertex), E(edge)
| 인접 행렬 | 인접 리스트 | |
| 공간복잡도 | O(V^2) | O(V+E) |
| 시간복잡도 (간선 1개 찾기) |
O(1) a[i][j] |
O(V) for(int j = 0; j < adj[j].size();j++){ cout << adj[i][j] << " "; } |
| 시간복잡도 (모든 간선 찾기) |
O(V^2) | O(V+E) |
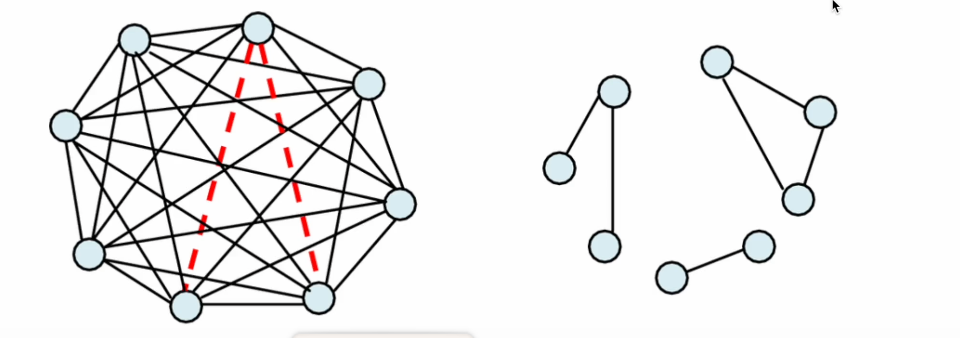
그래프가 희소할 때는 인접리스트, 조밀할 때는 인접행렬이 좋다!
그래프가 희소할 때 (sparse)할 때는 인접행렬이 인접리스트보다 메모리를 더 많이 써야 한다.
간선이 많지 않아서 인접행렬의 대부분의 요소가 0임에도 해당 부분을 포함해 2차원 배열을 만들어야 되기 때문.
그래프가 조밀할 때(dense)할 때는 인접행렬이 좋다.
어차피 다 연결되어 있기 때문에 메모리 효율성은 동일해지고
정점 i에서 정점 j까지의 간선이 있는 지 확인하는 속도가 더 빠르기 때문
보통은 인접리스트를 쓰기!
dense한 거 많이 안나오더라.
'Computer > 알고리즘' 카테고리의 다른 글
| 연결된 컴포넌트 (connected compoonent), Flood Fill (0) | 2024.02.07 |
|---|---|
| 맵(지도)과 방향벡터(direction vector) (1) | 2024.02.07 |
| 트리 (Tree Data Structure) 기초 , 이진트리와 이진탐색트리 (1) | 2024.02.05 |
| 그래프 이론 기초 (Graph, Vertex, Edge, Indegree, Outdegree, Weight) (1) | 2024.02.05 |
| 순열(Permutation)과 조합(Combination) (1) | 2024.01.30 |




